
分析 (1)由递推数列求数列的通项公式,适当的变形,证明数列{$\frac{1}{{a}_{n}}$}是等差数列,然后求数列{an}的通项公式.
(2)利用错位相减法求解数列的和即可.
解答 解:(1)数列{an}中,a1=1,an+1=$\frac{{a}_{n}}{{a}_{n}+1}$.可得,an+1an=an-an+1,
两边同除以anan+1,得$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=1,
所以{$\frac{1}{{a}_{n}}$}是等差数列,公差为1.$\frac{1}{{a}_{n}}$=1+(n-1)•1,
上述n-1个等式累加,
可得an=$\frac{1}{n}$.
(2)设bn=$\frac{1}{{2}^{n}•{a}_{n}}$=$\frac{n}{{2}^{n}}$,∴Tn=$\frac{1}{{2}^{1}}$+$\frac{2}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+…+$\frac{n}{{2}^{n}}$…①
$\frac{1}{2}$Tn=$\frac{1}{{2}^{2}}$+$\frac{2}{{2}^{3}}$+$\frac{3}{{2}^{4}}$+…+$\frac{n-1}{{2}^{n}}$$+\frac{n}{{2}^{n+1}}$,②
①-②,$\frac{1}{2}$Tn=$\frac{1}{2}+\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$$-\frac{1}{{2}^{n+1}}$=$\frac{\frac{1}{2}(1-(\frac{1}{2})^{n})}{1-\frac{1}{2}}$-$\frac{1}{{2}^{n+1}}$,
∴Tn=2-$\frac{6}{{2}^{n+1}}$.
点评 本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意错位相减求和法的合理运用.解答本题用到的累加法是求数列通项公式以及数列前n项和的重要方法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
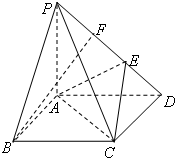 四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=$\sqrt{2}$,E,F为PD上两点,且PF=ED=$\frac{1}{3}$PD.
四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=$\sqrt{2}$,E,F为PD上两点,且PF=ED=$\frac{1}{3}$PD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数y=|x|有极大值,但无极小值 | B. | 函数y=|x|有极小值,但无极大值 | ||
| C. | 函数y=|x|既有极大值又有极小值 | D. | 函数y=|x|无极值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com