Question

1．已知$\overrightarrow{a}$=（$\sqrt{2}$，$\sqrt{2}$cos2（ωx+φ））（φ＞0，0＜φ＜$\frac{π}{2}$），$\overrightarrow{b}$=（$\frac{\sqrt{2}}{2}$，-$\frac{\sqrt{2}}{2}$），f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$，函数f（x）的图象过点B（1，2），点B与其相邻的最高点的距离为4．
（Ⅰ）求f（x）的单调递增区间；
（Ⅱ）计算f（1）+f（2）+…+f（2017）；
（Ⅲ）设函数g（x）=f（x）-m-1，试讨论函数g（x）在区间[0，3]上的零点个数．

Answer 1

分析 （Ⅰ）由数量积的坐标运算可得f（x），由题意求得ω=$\frac{π}{4}$，再由函数f（x）的图象过点B（1，2）列式求得φ．则函数解析式可求，由复合函数的单调性求得f（x）的单调递增区间；
（Ⅱ）由（Ⅰ）知，f（x）=1+sin$\frac{π}{2}x$，可得f（x）是周期为4的周期函数，且f（1）=2，f（2）=1，f（3）=0，f（4）=1．得到f（1）+f（2）+f（3）+f（4）=4．
进一步可得f（1）+f（2）+…+f（2017）=4×504+2=2018；
（Ⅲ）g（x）=f（x）-m-1=$sin\frac{π}{2}x-m$，函数g（x）在[0，3]上的零点个数，即为函数y=sin$\frac{π}{2}x$的图象与直线y=m在[0，3]上的交点个数．数形结合得答案．

解答 解：（Ⅰ）∵$\overrightarrow{a}$=（$\sqrt{2}$，$\sqrt{2}$cos2（ωx+φ）），$\overrightarrow{b}$=（$\frac{\sqrt{2}}{2}$，-$\frac{\sqrt{2}}{2}$），
∴f（x）=$\overrightarrow{a}•\overrightarrow{b}$=$\sqrt{2}×\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}×$$\sqrt{2}$cos2（ωx+φ）=1-cos2（ωx+φ）），
∴f（x）_max=2，则点B（1，2）为函数f（x）的图象的一个最高点．
∵点B与其相邻的最高点的距离为4，∴$\frac{2π}{2ω}=4$，得ω=$\frac{π}{4}$．
∵函数f（x）的图象过点B（1，2），∴$1-cos（\frac{π}{2}+2φ）=2$，即sin2φ=1．
∵0＜φ＜$\frac{π}{2}$，∴φ=$\frac{π}{4}$．
∴f（x）=1-cos2（$\frac{π}{4}x+\frac{π}{4}$）=1+sin$\frac{π}{2}x$，
由$2kπ-\frac{π}{2}≤\frac{π}{2}x≤2kπ+\frac{π}{2}$，得-1+4k≤x≤1+4k（k∈Z）．
∴f（x）的单调递增区间为[-1+4k，1+4k]，k∈Z；
（Ⅱ）由（Ⅰ）知，f（x）=1+sin$\frac{π}{2}x$，
∴f（x）是周期为4的周期函数，且f（1）=2，f（2）=1，f（3）=0，f（4）=1．
∴f（1）+f（2）+f（3）+f（4）=4．
而2017=4×504+1，
∴f（1）+f（2）+…+f（2017）=4×504+2=2018；
（Ⅲ）g（x）=f（x）-m-1=$sin\frac{π}{2}x-m$，函数g（x）在[0，3]上的零点个数，即为函数y=sin$\frac{π}{2}x$的图象
与直线y=m在[0，3]上的交点个数．
在同一直角坐标系内作出两个函数的图象如图：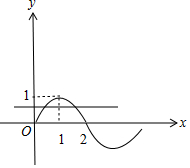
①当m＞1或m＜-1时，两函数的图象在[0，3]内无公共点；
②当-1≤m＜0或m=1时，两函数的图象在[0，3]内有一个共点；
③当0≤m＜1时，两函数的图象在[0，3]内有两个共点．
综上，当m＞1或m＜-1时，函数g（x）在[0，3]上无零点；
②当-1≤m＜0或m=1时，函数g（x）在[0，3]内有1个零点；
③当0≤m＜1时，函数g（x）在[0，3]内有2个零点．

点评 本题考查三角函数中的恒等变换应用，考查数量积的坐标运算，体现了数形结合的解题思想方法，是中档题．