
| A. | {x|x≥3或x≤1} | B. | {x|x≥4或x≤2} | C. | {x|x≥2或x≤1} | D. | {x|x≥4或x≤1}. |
分析 把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
解答 解:不等式|x-3|+|x-2|≥3,等价于 $\left\{\begin{array}{l}{x<2}\\{3-x+2-x≥3}\end{array}\right.$①,或$\left\{\begin{array}{l}{2≤x≤3}\\{3-x+x-2≥3}\end{array}\right.$②,或$\left\{\begin{array}{l}{x>3}\\{x-3+x-2≥3}\end{array}\right.$③.
解①求得x≤1,解②求得x∈∅,解③求得x≥4,
综上可得,不等式|x-3|+|x-2|≥3的解集是{x|x≥4或x≤1},
故选:D.
点评 本题主要考查绝对值的意义,绝对值不等式的解法,关键是去掉绝对值,化为与之等价的不等式组来解,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,求此点取自黑色部分的概率.
如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,求此点取自黑色部分的概率.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $2\sqrt{3}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
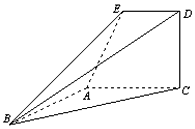 如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.
如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -3 | C. | 3 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com