练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在一次综合知识竞赛中，有两道填空题和两道解答题，填空题每题5分，解答题每题10分，某参赛者答对填空题的概率都是
    3
    4
    ，答对解答题的概率都是
    2
    3
    ，解答备题的结果是相互独立的．
    （Ⅰ）求该参赛者恰好答对一道题的概率；
    （Ⅱ）求该参赛者的总得分X的分布列及数学期望E（X）．
    考点：离散型随机变量的期望与方差,相互独立事件的概率乘法公式
    专题：概率与统计
    分析：（Ⅰ）设参赛者答对填空题为事件Ai（i=1，2），答对解答题为事件Bi（i=1，2），由此能求出该参赛者恰好答对一道题的概率．
    （Ⅱ）由题意知X可能的取值为0，5，10，15，20，25，30，分别求出P（X=0），P（X=5），P（X=10），P（X=15），P（X=20），P（X=25），P（X=30），由此能求出X的分布列和EX．
    解答： 解：（Ⅰ）设参赛者答对填空题为事件Ai（i=1，2），
    答对解答题为事件Bi（i=1，2），
    则有P（
    .
    A1
    .
    A2
    .
    B1
    B2    ）=P（
    .
    A1
    .
    A2
    B1
    .
    B2
    ）=（
    1
    4
    ）2×
    1
    3
    ×
    2
    3
    =
    1
    72
    ，
    P（A1
    .
    A2
    .
    B1
    .
    B2
    ）=P（
    .
    A1
    A2
    .
    B1
    .
    B2
    ）=
    1
    4
    ×
    3
    4
    ×(
    1
    3
    )2    =
    1
    48
    ，
    所以该参赛者恰好答对一道题的概率为：
    P=2×
    1
    72
    +2×
    1
    48
    =
    5
    72
    ．
    （Ⅱ）由题意知X可能的取值为0，5，10，15，20，25，30，
    P（X=0）=P（
    .
    A1
    .
    A2
    .
    B1
    .
    B2
    ）=（
    1
    4
    ）2•（
    1
    3
    ）2=
    1
    144
    ，
    P（X=5）=P(A1
    .
    A2
    .
    B1
    .
    B2
    ）+P（
    .
    A1
    A2
    .
    B1
    .
    B2
    ）=2×
    1
    4
    ×
    3
    4
    ×(
    1
    3
    )2    =
    1
    24
    ，
    P（X=10）=P(A1
    .
    A2
    .
    B1
    .
    B2
    )+P(
    .
    A1
    .
    A2
    .
    B1
    B2)    +P(
    .
    A1
    .
    A2
    B1
    .
    B2)

    =（
    3
    4
    ）2×（
    1
    3
    ）2+2×(
    1
    4
    )2    ×
    1
    3
    ×
    2
    3
    =
    13
    144
    ，
    P（X=15）=P(A1
    .
    A2
    .
    B1
    B2)    +P(A1
    .
    A2
    B1
    .
    B2
    )+    P(
    .
    A1
    A2
    .
    B1
    B2)    +P(
    .
    A1
    A2B1
    .
    B2
    )
    =4×
    1
    4
    ×
    3
    4
    ×
    2
    3
    ×
    1
    3
    =
    1
    6
    ．
    P（X=20）=P（A1A2
    .
    B1
    B2    ）+P（A1A2B1
    .
    B2
    ）+P（
    .
    A1
    .
    A2
    B1B2    ）
    =2×(
    3
    4
    )2×
    1
    3
    ×
    2
    3
    +(
    1
    4
    )2×(
    2
    3
    )2    =
    5
    18
    ，
    P（X=25）=P(
    .
    A1
    A2B1B2)    +P（A1
    .
    A2
    B1B2    ）
    =2×
    1
    4
    ×
    3
    4
    ×(
    2
    3
    )2    =
    1
    6
    ，
    P（X=30）=P（A1A2B1B2）=(
    2
    4
    )2(
    2
    3
    )2    =
    1
    4
    ，
    ∴X的分布列为：
     X  0  5  10  15  20  25 30 
     P  
    1
    144
    		  
    1
    24
    		  
    13
    144
    		  
    1
    6
    		  
    5
    18
    		  
    1
    6
    1
    4
     
    ∴EX=0×
    1
    144
    +5×
    1
    24
    +10×
    13
    144
    +15×
    1
    6
    +20×
    5
    18
    +25×
    1
    6
    +30×
    1
    4
    =
    125
    6
    ．
    点评：本题考查概率的求法，考查离散型随机事件的分布列和数学期望的求法，是中档题，在历年高考中都是必考题型．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知i是虚数单位，若复数z满足i=
    1-i
    z
    ，则z=（　　）
    A、-1-iB、-1+i
    C、1-iD、1+i

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列命题：①321＜325； ②321＞325；③loga6＜loga7（0＜a＜1）；④loga6＞loga7（0＜a＜1）； 正确的是（　　）
    A、①③B、①④C、②③D、②④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设集合A={x|0＜x≤3}，B={x|x＜-1，或x＞2}，则A∩B=（　　）
    A、（2，3]
    B、（-∞，-1）∪（0，+∞）
    C、（-1，3]
    D、（-∞，0）∪（2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知命题p：对任意的区间[1，2]内的实数x，x2-a≥0恒成立；命题q：方程x2+2ax+2-a=0有实根．若命题p，q都是真命题，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

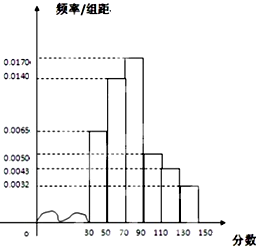    衡水市为“市中学生知识竞赛”进行选拔性测试，且规定：成绩大于或等于90分的有参赛资格，90分以下（不包括90分）的则被淘汰．若现有500人参加测试，学生成绩的频率分布直方图如图：
    （Ⅰ）求获得参赛资格的人数；
    （Ⅱ）根据频率直方图，估算这500名学生测试的平均成绩；
    （Ⅲ）若知识竞赛分初赛和复赛，在初赛中每人最多有5次选题答题的机会，累计答对3题或答错3题即终止，答对3题者方可参加复赛，已知参赛者甲答对每一个问题的概率都相同，并且相互之间没有影响，已知他连续两次答错的概率为
    1
    9
    ，求甲在初赛中答题个数的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某同学完成一项任务共用去9h，他记录的完成工作量的百分数如下表：
    时间/h 1 2 3 4 5 6 7 8 9
    完成的百分数/% 15 30 45 60 60 70 80 90 100
    （1）如果用T（x）表示x（h）后他完成工作量的百分数，那么T（5）是多少？求出T（x），并画出其图象；
    （2）如果该同学在早晨8时开始工作，什么时候他在休息？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    甲、乙、丙、丁、戊5名学生进行劳动技术比赛，决出第一名至第五名的名次．比赛之后甲乙两位参赛者去询问成绩，回答者对甲说“根遗憾，你和乙都投有得到冠军”，对乙说“你当然不会是最差的”．
    （Ⅰ）从上述回答分析，5人的名次排列可能有多少种不同的情况；
    （Ⅱ）比赛组委会规定，第一名获奖金1000元，第二名获奖金800元，第三名获奖金600元，第四及第五名没有奖金，求丙获奖金数的期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若在平面直角坐标系内过点P(1，
    		3
    )    且与原点的距离为d的直线有两条，则d的取值范围是
     
    ．

    查看答案和解析>>

    同步练习册答案