
分析 (I)利用向量的坐标运算、模的计算公式即可得出;
(Ⅱ)与$\overrightarrow{a}$平行的单位向量=$\frac{\overrightarrow{a}}{|\overrightarrow{a}|}$,即可得出.
解答 解:(Ⅰ)∵向量$\overrightarrow{a}$的始点为A(-2,4),终点为B(2,1),
∴向量$\overrightarrow{a}$=(2,1)-(-2,4)=(4,-3),
∴向量$|\overrightarrow{a}|$=$\sqrt{{4^2}+{{(-3)}^2}}$=5.
(Ⅱ)与$\overrightarrow{a}$平行的单位向量=$\frac{\overrightarrow{a}}{|\overrightarrow{a}|}$=$\frac{1}{5}$(4,-3)=($\frac{4}{5}$,-$\frac{3}{5}$).
点评 本题考查了向量的坐标运算、模的计算公式、与$\overrightarrow{a}$平行的单位向量=$\frac{\overrightarrow{a}}{|\overrightarrow{a}|}$,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\sqrt{3}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2kπ-$\frac{4}{3}$π,2kπ-$\frac{2}{3}$π](k∈Z) | B. | [4kπ-$\frac{4}{3}$π,4kπ+$\frac{2}{3}$π](k∈Z) | ||
| C. | [$2kπ+\frac{2}{3}π,2kπ+\frac{8}{3}π$](k∈Z) | D. | [$4kπ+\frac{2}{3}π,4kπ+\frac{8}{3}π}]$](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $arcsin\frac{{\sqrt{3}}}{5}$ | B. | arcsin(-$\frac{\sqrt{3}}{5}$) | C. | π-arcsin$\frac{{\sqrt{3}}}{5}$ | D. | $\frac{π}{2}+arcsin\frac{{\sqrt{3}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1] | B. | [-2,-1] | C. | ∅ | D. | [-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
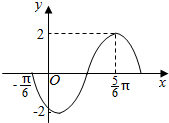 已知函数f(x)=2sin(ωx+φ),(ω>0,0<φ<2π)的部分图象如图所示,则f(x)的表达式为( )
已知函数f(x)=2sin(ωx+φ),(ω>0,0<φ<2π)的部分图象如图所示,则f(x)的表达式为( )| A. | $f(x)=2sin(\frac{4}{3}x+\frac{2}{9}π)$ | B. | $f(x)=2sin(\frac{4}{3}x+\frac{25}{18}π)$ | ||
| C. | $f(x)=2sin(\frac{3}{2}x+\frac{π}{4})$ | D. | $f(x)=2sin(\frac{3}{2}x+\frac{5}{4}π)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{32π}{3}$ | B. | 4π | C. | 2π | D. | $\frac{4π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com