
分析 ①根据复合命题真假以及充分条件和必要条件的定义进行判断.
②根据含有量词的命题的否定进行判断.
③根据转化法结合一元二次函数的单调性进行判断.
④根据数列构造函数,判断函数的单调性进行判断.
解答 解:①若“p∧q”为真,则p,q同时为真,则“p∨q”为真,
反之若“p∨q”为真,则p,q至少有一个为真,则“p∧q”不一定为真,
故“p∧q”为真的一个必要不充分条件是“p∨q”为真,正确,故①正确,
②若p:$\frac{1}{x}$>0,则¬p:$\frac{1}{x}$≤0或x=0,故②错误,
③若实数a,b满足$\sqrt{a}$+$\sqrt{b}$=1,
由$\sqrt{a}$+$\sqrt{b}$=1得$\sqrt{b}$=1-$\sqrt{a}$≥0,则0≤a≤1,
则b=(1-$\sqrt{a}$)2=1-2$\sqrt{a}$+a,
则a+b=2a-2$\sqrt{a}$+1=2($\sqrt{a}$)2-2$\sqrt{a}$+1=2($\sqrt{a}$-$\frac{1}{2}$)2+$\frac{1}{2}$,
∵0≤a≤1,∴0≤$\sqrt{a}$≤1,
即当$\sqrt{a}$=$\frac{1}{2}$时,a+b取得最小值$\frac{1}{2}$,
当$\sqrt{a}$=0或1时,a+b取得最大值1,
即$\frac{1}{2}$≤a+b≤1成立,故③正确,
④$\frac{{2}^{n}}{({2}^{n}+1)^{2}}$=$\frac{{2}^{n}}{({2}^{n})^{2}+2•{2}^{n}+1}$=$\frac{1}{{2}^{n}+\frac{1}{{2}^{n}}+2}$,
∵n∈N*,
∴2n≥2,则y=2n+$\frac{1}{{2}^{n}}$在[1,+∞)上是增函数,则y=$\frac{1}{{2}^{n}+\frac{1}{{2}^{n}}+2}$在[1,+∞)上是减函数,
∴当n=1时,y=$\frac{1}{{2}^{n}+\frac{1}{{2}^{n}}+2}$取得最大值,此时y=$\frac{2}{(2+1)^{2}}$=$\frac{2}{9}$,故④正确.
点评 本题主要考查命题的真假判断,涉及的知识点交点,综合性较强,有一定的难度.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | $-\frac{2}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
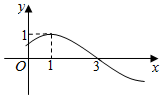 函数y=sin(ωx+φ)(x∈R,ω>0,-π<φ<π)的部分图象如图,则该函数的解析式为y=sin($\frac{π}{4}$x$+\frac{π}{4}$).
函数y=sin(ωx+φ)(x∈R,ω>0,-π<φ<π)的部分图象如图,则该函数的解析式为y=sin($\frac{π}{4}$x$+\frac{π}{4}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
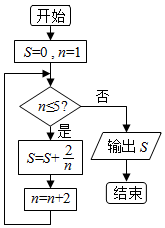
| A. | $\frac{8}{3}$ | B. | $\frac{46}{15}$ | C. | $\frac{25}{6}$ | D. | $\frac{137}{30}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com