
| A. | -3 | B. | -10 | C. | 4 | D. | 10 |
分析 画出约束条件的可行域,转化目标函数的解析式,利用目标函数的最大值,判断最优解,代入约束条件求解即可.
解答 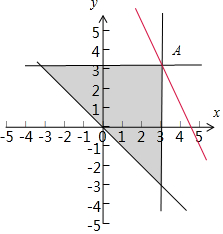 解:不等式组约束条件$\left\{\begin{array}{l}{x-3≤0}\\{y-a≤0}\\{x+y≥0}\end{array}\right.$,它的可行域如图:
解:不等式组约束条件$\left\{\begin{array}{l}{x-3≤0}\\{y-a≤0}\\{x+y≥0}\end{array}\right.$,它的可行域如图:
O为坐标原点,点A的坐标为(2,1),点P(x,y),
z=$\overrightarrow{OP}•\overrightarrow{OM}$=2x+y,$\overrightarrow{OP}•\overrightarrow{OM}$的最大值为10,
可得2x+y=10,如图:红线,经过可行域的A,
由:$\left\{\begin{array}{l}{2x+y=10}\\{x=3}\end{array}\right.$可得A(3,4),
(3,4)代入y=a,可得a=4.
故选:C.
点评 本题考查线性规划的应用,考查转化思想以及数形结合思想的应用,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
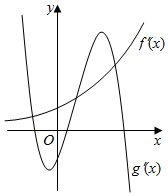 定义在R上的函数f(x)和g(x),其各自导函数f′(x)f和g′(x)的图象如图所示,则函数F(x)=f(x)-g(x)极值点的情况是( )
定义在R上的函数f(x)和g(x),其各自导函数f′(x)f和g′(x)的图象如图所示,则函数F(x)=f(x)-g(x)极值点的情况是( )| A. | 只有三个极大值点,无极小值点 | B. | 有两个极大值点,一个极小值点 | ||
| C. | 有一个极大值点,两个极小值点 | D. | 无极大值点,只有三个极小值点 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | ab<b2 | C. | ac2<bc2 | D. | |a|>|b| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,sinx0+cos0=$\frac{3}{2}$ | |
| B. | 已知X服从正态分布N(0,σ2),且p(-2<X≤2)=0.6,则P(X>2)=0.2 | |
| C. | 已知a,b为实数,则a+b=0的充要条件是$\frac{a}{b}$=-1 | |
| D. | 命题“?x∈R,x2-x+1>0”的否定是“?x0∈R,x2-x+1<0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com