
| A. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{y}^{2}}{2}$-$\frac{{x}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1 | D. | $\frac{{y}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1 |
分析 由椭圆方程求出椭圆及双曲线的半焦距,设出与双曲线$\frac{{x}^{2}}{2}$-y2=1有相同渐近线的双曲线方程为$\frac{{x}^{2}}{2}$-y2=λ,化为标准方程,结合双曲线中的隐含条件求得λ值,则答案可求.
解答 解:由$\frac{y^2}{8}+\frac{x^2}{2}=1$,得a2=8,b2=2,
∴c2=6,得c=$\sqrt{6}$,
即椭圆的半焦距为$\sqrt{6}$.
设与双曲线$\frac{{x}^{2}}{2}$-y2=1有相同渐近线的双曲线方程为$\frac{{x}^{2}}{2}$-y2=λ,
∵所求双曲线的焦点在y轴上,则λ<0,
双曲线方程化为:$\frac{{y}^{2}}{-λ}-\frac{{x}^{2}}{-2λ}=1$,
设双曲线的实半轴长为m,虚半轴长为n,
则m2=-λ,n2=-2λ,
∴${m}^{2}+{n}^{2}=-λ-2λ=(\sqrt{6})^{2}$,解得:λ=-2.
∴所求双曲线的方程为$\frac{{y}^{2}}{2}-\frac{{x}^{2}}{4}=1$.
故选:B.
点评 本题考查双曲线标准方程的求法,掌握与双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$有共同渐近线的双曲线方程的设法是关键,是中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
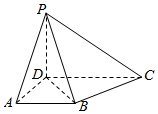 在四棱锥P-ABCD中,AD⊥平面PDC,PD⊥DC,底面ABCD是梯形,AB∥DC,AB=AD=PD=1,CD=2.
在四棱锥P-ABCD中,AD⊥平面PDC,PD⊥DC,底面ABCD是梯形,AB∥DC,AB=AD=PD=1,CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3a2cosa+10ax2 | B. | 3a2cosa+10ax2+10a2x | ||
| C. | a3sina+10a2x | D. | 10a2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com