
| 房型 | 特大套 | 大套 | 经济适用房 |
| 舒适 | 100 | 150 | x |
| 标准 | 300 | y | 600 |
分析 (1)由分层抽样原理列出方程求出y、x的值;
(2)设至少有一套舒适型套房记为事件A,
求出事件A发生的个数与基本事件的总和,计算所求的概率;
(3)根据题意得ξ可能的取值,计算对应的概率,
写出ξ的分布列,求出数学期望值.
解答 解:(1)由题设知$\frac{10}{400}$=$\frac{15}{y+150}$=$\frac{25}{x+600}$,
解得y=450,x=400;
(2)设至少有一套舒适型套房记为事件A,事件A发生的个数为:
$C_2^1C_3^1+C_2^2=7$,
基本事件的总和为$C_5^2$,
故所求的概率为$P(A)=\frac{7}{10}$;
(3)根据题意,ξ可能的取值为1,2,3,4,5,
则$P(ξ=1)=\frac{C_2^1}{C_6^1}=\frac{1}{3}$,
$P(ξ=2)=\frac{C_4^1C_2^1}{C_6^1C_5^1}=\frac{4}{15}$,
$P(ξ=3)=\frac{C_4^1C_3^1C_2^1}{C_6^1C_5^1C_4^1}=\frac{1}{5}$,
$P(ξ=4)=\frac{C_4^1C_3^1C_2^1C_2^1}{C_6^1C_5^1C_4^1C_3^1}=\frac{2}{15}$,
$P({ξ=5})=\frac{1}{15}$;
所以ξ的分布列为:
| ξ | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{1}{3}$ | $\frac{4}{15}$ | $\frac{1}{5}$ | $\frac{2}{15}$ | $\frac{1}{15}$ |
点评 本题考查了离散型随机变量的分布列与数学期望的计算问题,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
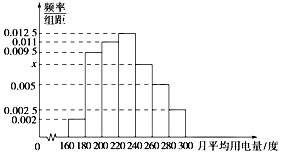 节能减排以来,兰州市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
节能减排以来,兰州市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 培养液处理 | 未处理 | 合计 | |
| 青花病 | 30 | 224 | 254 |
| 无青花病 | 24 | 1355 | 1379 |
| 合计 | 54 | 1579 | 1633 |
| P(K2≥k) | 0.05 | 0.01 | 0.005 | 0.001 |
| k | 3.841 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com