Question

8．过圆x²+y²=25内一点P（$\sqrt{15}$，0）作倾斜角互补的直线AC和BD，分别与圆交于A、C和B、D，则四边形ABCD面积的最大值为（　　）

• A． 40$\sqrt{3}$
• B． $\frac{80\sqrt{3}}{3}$
• C． 40$\sqrt{2}$
• D． $\frac{80\sqrt{2}}{3}$

Answer 1

分析 由题意画出图形，设AC的倾斜角为θ（0＜θ＜$\frac{π}{2}$），可得AC：y=tanθ（x-$\sqrt{15}$）．再设A（x₁，y₁），C（x₂，y₂），联立直线方程与圆的方程，利用根与系数的关系结合梯形面积公式可得S_ABCD=$\frac{40ta{n}^{3}θ-100tanθ}{（1+ta{n}^{2}θ）^{2}}$．换元后利用导数求最值．

解答 解：如图，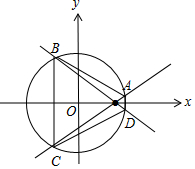

设AC的倾斜角为θ（0＜θ＜$\frac{π}{2}$），
则AC：y=tanθ（x-$\sqrt{15}$）．
设A（x₁，y₁），C（x₂，y₂），
由对称性可得：${S}_{ABCD}=2×\frac{1}{2}（{y}_{1}-{y}_{2}）（{x}_{1}-{x}_{2}）$
=$tanθ（{x}_{1}-{x}_{2}）^{2}$=$tanθ[（{x}_{1}+{x}_{2}）^{2}-4{x}_{1}{x}_{2}]$．
联立$\left\{\begin{array}{l}{y=x•tanθ-\sqrt{15}tanθ}\\{{x}^{2}+{y}^{2}=25}\end{array}\right.$，得$（1+ta{n}^{2}θ）{x}^{2}-2\sqrt{15}x•ta{n}^{2}θ+15ta{n}^{2}θ-25=0$．
∴${x}_{1}+{x}_{2}=\frac{2\sqrt{15}ta{n}^{2}θ}{1+ta{n}^{2}θ}$，${x}_{1}{x}_{2}=\frac{15ta{n}^{2}θ-25}{1+ta{n}^{2}θ}$．
则S_ABCD=$tanθ[\frac{60ta{n}^{4}θ}{（1+ta{n}^{2}θ）^{2}}-\frac{60ta{n}^{2}θ-100}{1+ta{n}^{2}θ}]$=$\frac{40ta{n}^{3}θ-100tanθ}{（1+ta{n}^{2}θ）^{2}}$．
令tanθ=k（k＞0），
则S=$\frac{40{k}^{3}-100k}{（1+{k}^{2}）^{2}}$，∴S′=$-20（2{k}^{2}-1）•\frac{{k}^{2}+5}{（1+{k}^{2}）^{2}}$．
∴当k∈（0，$\frac{\sqrt{2}}{2}$）时，S′＞0，当k∈（$\frac{\sqrt{2}}{2}，+∞$）时，S′＜0，
∴当k=$\frac{\sqrt{2}}{2}$时，${S}_{max}=\frac{80\sqrt{2}}{3}$．
故选：D．

点评 本题主要考查直线和圆的相关知识，三角函数的最值问题，考查换元法的思想，以及运算能力，训练了利用导数求函数的最值，属于中档题