
分析 (1)分类讨论,当λ=1时,f(x)=x2(x-a)-(x+a)3=-a(4x2+3ax+a2);由二次函数的性质判断;当λ≠1时,则必有一个零点是极值点;不妨设该零点为x0,
从而可得f(x0)=x02(x0-a)-λ(x0+a)3=0,再求导得f′(x0)=3x02-2ax0-3λ(x0+a)2=0,从而解得x0=0或x0=$\frac{a}{2}$;再检验即可;
(2)求导f′(x)=3x2-2ax-3λ(x+a)2=3(1-λ)x2-2a(1+3λ)x-3λa2,分类讨论;
①当λ=1时,f′(x)=-8ax-3a2;从而确定极大值点g(λ)=-$\frac{3}{8}$a;
②当λ≠1时,1-λ≠0,令△=4a2(1+3λ)2+36(1-λ)λa2=4a2(1+15λ),讨论二次项系数及判断式的正负以确定f′(x)的正负,从而确定极大值点g(λ);可得λ>-$\frac{1}{15}$且λ≠1时,g(λ)=$\frac{1+3λ-\sqrt{1+15λ}}{3(1-λ)}$a;再利用换元法令$\sqrt{1+15λ}$=t,则λ=$\frac{{t}^{2}-1}{15}$,(t>0且t≠4);从而得g(λ)=h(t)=$\frac{1-t}{t+4}$a;从而求取值范围.
解答 解:(1)当λ=1时,f(x)=x2(x-a)-(x+a)3
=-a(4x2+3ax+a2);
∵-a<0,△=(3a)2-16a2=-7a2<0,
∴f(x)<0恒成立;故没有零点;
当λ≠1时,函数f(x)恰有两个零点;
则必有一个零点是极值点;
不妨设该零点为x0,
则f(x0)=x02(x0-a)-λ(x0+a)3=0,
即x02(x0-a)=λ(x0+a)3,①
又f′(x)=3x2-2ax-3λ(x+a)2
故f′(x0)=3x02-2ax0-3λ(x0+a)2=0,②
由①②化简可得,
x0=0或x0=$\frac{a}{2}$;
经检验,当x0=0时成立,此时λ=0;
当x0=$\frac{a}{2}$时也成立,此时λ=-$\frac{1}{27}$;
故λ=0或λ=-$\frac{1}{27}$;
(2)∵f′(x)=3x2-2ax-3λ(x+a)2
=3(1-λ)x2-2a(1+3λ)x-3λa2;
①当λ=1时,f′(x)=-8ax-3a2;
则x<-$\frac{3}{8}$a时,f′(x)>0,x>-$\frac{3}{8}$a时,f′(x)<0;
故g(λ)=-$\frac{3}{8}$a;
②当λ≠1时,1-λ≠0,令△=4a2(1+3λ)2+36(1-λ)λa2=4a2(1+15λ),
(i)当λ≤-$\frac{1}{15}$时,1-λ>0且△≤0,故f′(x)≥0,
函数f(x)是R上的增函数,函数f(x)无极值点;
(ii)当-$\frac{1}{15}$<λ<1时,1-λ>0且△>0,
由f′(x)=0解得,
x1=$\frac{1+3λ-\sqrt{1+15λ}}{3(1-λ)}$a,x2=$\frac{1+3λ+\sqrt{1+15λ}}{3(1-λ)}$a;
注意到x1<x2,且x<x1时,f′(x)>0,x1<x<x2时,f′(x)<0,x>x2时,f′(x)>0;
故g(λ)=$\frac{1+3λ-\sqrt{1+15λ}}{3(1-λ)}$a;
(iii)当λ>1时,1-λ<0且△>0,
由f′(x)=0解得,
x1=$\frac{1+3λ-\sqrt{1+15λ}}{3(1-λ)}$a,x2=$\frac{1+3λ+\sqrt{1+15λ}}{3(1-λ)}$a;
注意到x1>x2,且x<x2时,f′(x)<0,x2<x<x1时,f′(x)>0,x>x1时,f′(x)<0;
故g(λ)=$\frac{1+3λ-\sqrt{1+15λ}}{3(1-λ)}$a;
综上所述,λ>-$\frac{1}{15}$且λ≠1时,
g(λ)=$\frac{1+3λ-\sqrt{1+15λ}}{3(1-λ)}$a;
令$\sqrt{1+15λ}$=t,则λ=$\frac{{t}^{2}-1}{15}$,(t>0且t≠4);
将λ=$\frac{{t}^{2}-1}{15}$代入g(λ)=$\frac{1+3λ-\sqrt{1+15λ}}{3(1-λ)}$a得,
g(λ)=h(t)=$\frac{1-t}{t+4}$a;
当λ=1时,t=4,g(λ)=-$\frac{3}{8}$a,上式也成立;
∵h(t)=$\frac{1-t}{t+4}$a=(-1+$\frac{5}{t+4}$)a是(0,+∞)上的减函数,
由t>0得-a<h(t)<$\frac{a}{4}$,
即g(λ)的取值范围是(-a,$\frac{a}{4}$).
点评 本题考查了导数的综合应用及分类讨论的思想应用,本题难点在于分类讨论的情况比较多,讨论的依据也比较多,属于难题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:解答题
 某医院眼科某天测量300名求医者的视力情况,得到频率分布直方图如图所示,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列.
某医院眼科某天测量300名求医者的视力情况,得到频率分布直方图如图所示,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
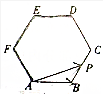 如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=k,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间为[$-\frac{k}{2}$,0]∪[k,$\frac{3}{2}{k}^{2}$].
如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=k,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间为[$-\frac{k}{2}$,0]∪[k,$\frac{3}{2}{k}^{2}$].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com