
| 2 | ||
|
| 18-3r |
| 2 |
| C | r 9 |
| 2 | ||
|
| C | r 9 |
| 3 |
| 2 |
| r |
| 2 |
| 18-3r |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:[20,25),{25,30),[30,35),[35,40)[40,45].
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:[20,25),{25,30),[30,35),[35,40)[40,45].查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在直四棱ABCD-A1B1C1D1中(侧棱与底面垂直的棱柱叫直棱柱),底面ABCD是边长为4的菱形,且∠DAB=60°,AA1=2
如图,在直四棱ABCD-A1B1C1D1中(侧棱与底面垂直的棱柱叫直棱柱),底面ABCD是边长为4的菱形,且∠DAB=60°,AA1=2| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
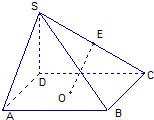 已知四棱锥S-ABCD中,底面ABCD为正方形,SD⊥DA,E为SC的中点,O为正方形ABCD的中心,AB=SD=6.
已知四棱锥S-ABCD中,底面ABCD为正方形,SD⊥DA,E为SC的中点,O为正方形ABCD的中心,AB=SD=6.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com