
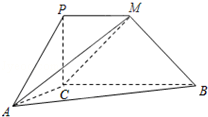
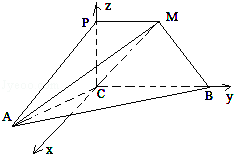
 如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=PC=AC=1,BC=2,又∠ACB=120°,AB⊥PC.
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=PC=AC=1,BC=2,又∠ACB=120°,AB⊥PC.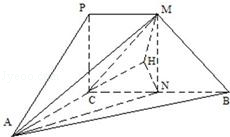
| ||
| 2 |
| ||
| 2 |
| NH2+MN2 |
(
|
| ||
| 2 |
| NH |
| MH |
| ||
| 7 |
| ||
| 2 |
| 1 |
| 2 |
| CM |
| CA |
| ||
| 2 |
| 1 |
| 2 |
| n |
| n |
| CM |
| n |
| CA |
|
| n |
| 3 |
| 3 |
| m |
| m |
| n |
-
| ||
1×
|
| ||
| 7 |
| ||
| 7 |


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
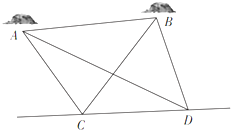 如图,A,B是海平面上的两个小岛,为测量A,B两岛间的距离,测量船以15海里/小时的速度沿既定直线CD航行,在t1时刻航行到C处,测得∠ACB=75°,∠ACD=120°,1小时后,测量船到达D处,测得∠ADC=30°,∠ADB=45°,求A,B两小岛间的距离.(注:A、B、C、D四点共面)
如图,A,B是海平面上的两个小岛,为测量A,B两岛间的距离,测量船以15海里/小时的速度沿既定直线CD航行,在t1时刻航行到C处,测得∠ACB=75°,∠ACD=120°,1小时后,测量船到达D处,测得∠ADC=30°,∠ADB=45°,求A,B两小岛间的距离.(注:A、B、C、D四点共面)查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| kπ |
| 6 |
| 1 |
| 2 |
| b |
| ||
| 2 |
| kπ |
| 6 |
| a |
| b |
| 2 |
| k |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,且AB=2
如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,且AB=2| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点.不包括右端点.如第一组表示收入在[1000,1500)
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点.不包括右端点.如第一组表示收入在[1000,1500)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com