
分析 (1)根据递推公式求出a2,a3,a4;
(2)由此可以猜想an=2n-1,根据数学归纳法证明即可;
(3)根据错位相减法求出Tn=3-$\frac{1}{{2}^{n-2}}$-$\frac{2n-1}{{2}^{n}}$,再利用放缩法即可证明.
解答 解:(1)a1=1且4Sn=n(an+an+1),
当n=1时,4S1=a1+a2,∴a2=3a1=3,
当n=2时,4S2=4(a1+a2)=2(a2+a3),∴a3=2a1+a2=5a1=5,
当n=3时,4S3=4(a1+a2+a3)=3(a3+a4),∴a4=7a1=7,
(2)由此可以猜想an=2n-1,下边用数学归纳法证明:
①当n=1时,a1=2×1-1=1,猜想成立.
②假设当n=k时猜想成立,即ak=2k-1,
∵Sn=$\frac{n(2n-1+1)}{2}$=n2,
那么当n=k+1时,∵4Sn=n(an+an+1),
∴4Sk=k(ak+ak+1),
∴4k2=k(2k-1+ak+1),
∴ak+1=2k+1,
∴当n=k+1时,猜想仍然成立.
综合①②可得,猜想对任意正整数都成立,an=2n-1,n∈N+成立,
(3)∵数列{$\frac{{a}_{n}}{{2}^{n}}$}的前n项和为Tn,
∴Tn=$\frac{1}{2}$+$\frac{3}{{2}^{2}}$+$\frac{5}{{2}^{3}}$+…+$\frac{2n-1}{{2}^{n}}$,
∴$\frac{1}{2}$Tn=$\frac{1}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+$\frac{5}{{2}^{4}}$+…+$\frac{2n-3}{{2}^{n}}$+$\frac{2n-1}{{2}^{n+1}}$,
∴$\frac{1}{2}$Tn=$\frac{1}{2}$+2•$\frac{1}{{2}^{2}}$+2•$\frac{1}{{2}^{3}}$+…+2•$\frac{1}{{2}^{n}}$-$\frac{2n-1}{{2}^{n+1}}$=$\frac{1}{2}$-1+2($\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$)-$\frac{2n-1}{{2}^{n+1}}$=-$\frac{1}{2}$+2•$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-$\frac{2n-1}{{2}^{n+1}}$=$\frac{3}{2}$-$\frac{1}{{2}^{n-1}}$-$\frac{2n-1}{{2}^{n+1}}$,
∴Tn=3-$\frac{1}{{2}^{n-2}}$-$\frac{2n-1}{{2}^{n}}$<3.
点评 本题考查了数列的递推公式和以及等差数列的前n项和,和数学归纳法和错位相减法求前n项和,培养了学生的运算能力和划归能力,属于难题.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
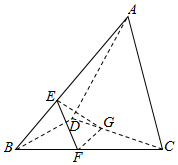 如图,A-BCD是一个不透明的三棱锥木块,点E,F,G分别在AB,BC,CD上,且F,G是BC,CD的中点,BE:EA=1:2,
如图,A-BCD是一个不透明的三棱锥木块,点E,F,G分别在AB,BC,CD上,且F,G是BC,CD的中点,BE:EA=1:2,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?a∈R,f(x)是偶函数 | B. | ?a∈R,f(x)是奇函数 | ||
| C. | ?a∈(0,+∞),f(x)在(-∞,0)上是增函数 | D. | ?a∈(0,+∞),f(x)在(0,+∞)上是减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| A1 | A2 | A3 | |
| B1 | $\frac{5}{6}$ | $\frac{3}{4}$ | $\frac{1}{3}$ |
| B2 | $\frac{2}{3}$ | $\frac{2}{3}$ | $\frac{1}{2}$ |
| B3 | $\frac{6}{7}$ | $\frac{5}{6}$ | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | 0 | D. | -l |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{2}$i | D. | $-\frac{1}{2}i$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com