
为预防禽流感病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:
|
| A组 | B组 | C组 |
| 疫苗有效 | 673 | x | y |
| 疫苗无效 | 77 | 90 | z |
已知在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33.
(1)求x的值;
(2)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取多少个?
(3)已知y≥465,z≥30,求不能通过测试的概率.
(1)∵在全体样本中随机抽取1个,抽取B组疫苗有效的概率约为其频率,即 =0.33,
=0.33,
∴x=660.
(2)C组样本个数为y+z=2000-(673+77+660+90)=500,
现用分层抽样的方法在全体样本中抽取360个测试结果,则应在C组抽取个数为 ×500=90.
×500=90.
(3)设测试不能通过的事件为A,C组疫苗有效与无效的可能的情况记为(y,z),由(2)知y+z=500,且y,z∈N,所有基本事件有:(465,35),(466,34),(467,33),(468,32),(469,31),(470,30)共6个,
若测试不能通过,则77+90+z>2000×(1-0.9),即z>33,
事件A包含的基本事件有:(465,35),(466,34)共2个,∴P(A)= =
= ,故不能通过测试的概率为
,故不能通过测试的概率为 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
已知点A(2,0),抛物线C:x2=4y的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N,则|FM|:|MN|=( )
A.2: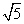 B.1:2
B.1:2
C.1: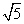 D.1:3
D.1:3
查看答案和解析>>
科目:高中数学 来源: 题型:
为了了解参加一次知识竞赛的3204名学生的成绩,决定采用系统抽样的方法抽取一个容量为80的样本,那么总体中应随机剔除的个体数目是( )
A.2 B.3
C.4 D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
用系统抽样法要从160名学生中抽取容量为20的样本,将160名学生随机地从1~160编号,按编号顺序平均分成20组(1~8号,9~16号,…,153~160号),若第16组抽出的号码为126,则第1组中用抽签方法确定的号码是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
某公路设计院有工程师6人,技术员12人,技工18人,要从这些人中抽取n个人参加市里召开的科学技术大会.如果采用系统抽样和分层抽样的方法抽取,不用剔除个体;如果参会人数增加1个,则在采用系统抽样时,需要在总体中先剔除1个个体,则n=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是( )
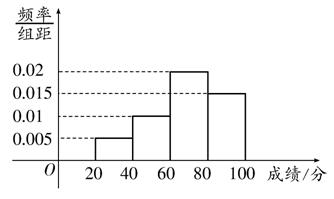
A.45 B.50
C.55 D.60
查看答案和解析>>
科目:高中数学 来源: 题型:
PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5μm的颗粒物,也称为可入肺颗粒物,根据现行国家标准GB3095—2012,PM2.5日均值在35微克/m3以下空气质量为一级;在35微克/m3~75微克/m3之间空气质量为二级;在75微克/m3以上空气质量为超标.从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取12天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶):
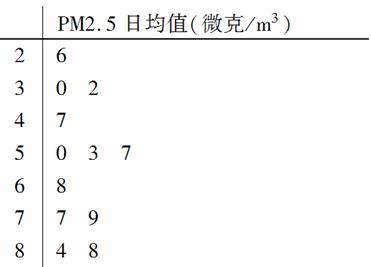
(1)求空气质量为超标的数据的平均数与方差;
(2)从空气质量为二级的数据中任取2个,求这2个数据的和小于100的概率;
(3)以这12天的PM2.5日均值来估计2012年的空气质量情况,估计2012年(按366天计算)中大约有多少天的空气质量达到一级或二级.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com