
分析 对任意的m,n∈N*,均有(n-m)Sn+m=(n+m)(Sn-Sm),令m=1,则(n-1)Sn+1=(n+1)(Sn-a1).化为nan+1=Sn+1+Sn-(n+1)a1,n≥2时,(n-1)an=Sn+Sn-1-na1,化为(n-1)an+1-nan=-a1,利用递推关系可得:an+1+an-1=2an.因此数列{an}是等差数列.由a2016=3000=a1+2015d,即3000-a1=2015d,由于数列{an}的各项均为正整数,可得d=0或1.即可得出.
解答 解:∵对任意的m,n∈N*,均有(n-m)Sn+m=(n+m)(Sn-Sm),
令m=1,则(n-1)Sn+1=(n+1)(Sn-a1).化为nan+1=Sn+1+Sn-(n+1)a1,
n≥2时,(n-1)an=Sn+Sn-1-na1,
∴nan+1-(n-1)an=an+1+an-a1,
∴(n-1)an+1-nan=-a1,
(n-2)an-(n-1)an-1=-a1,
∴(n-1)(an+1+an-1)=2(n-1)an,
∴an+1+an-1=2an.
∴数列{an}是等差数列.
∵a2016=3000=a1+2015d,即3000-a1=2015d,
∵数列{an}的各项均为正整数,∴d=0或1.
若d=0,则an=a2016=2016.
若d=1,则a1=885,∴an=985+(n-1)=984+n.
故答案为:984+n或3000.
点评 本题考查了递推关系、等差数列的通项公式、分类讨论方法,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{100}{101}$ | B. | $\frac{200}{101}$ | C. | $\frac{99}{100}$ | D. | $\frac{198}{100}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{1}{18}$ | C. | $\frac{2}{21}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在公比为2的等比数列{an}中,a2与a5的等差中项是9$\sqrt{3}$.
在公比为2的等比数列{an}中,a2与a5的等差中项是9$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
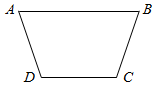 某地修建防洪渠道,其直截面图是等腰梯形ABCD(如图),底CD=40,腰AD=40,为使防洪渠道的通水量最大,应将防洪渠道的上口AB的宽设计为多少?
某地修建防洪渠道,其直截面图是等腰梯形ABCD(如图),底CD=40,腰AD=40,为使防洪渠道的通水量最大,应将防洪渠道的上口AB的宽设计为多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com