
设函数f(x)=x-ln(x+m)其中常数m为整数。
(1)当m为何值时,f(x)≥ 0;
0;
(2)定理:若g(x)在[a、b]上连续,且g(a)与g(b)异号,则至少存在一点x0∈(a、b),使g(x0)=0.试用上述定理证明:当整数m>1时,方程f(x)=0,在[e-m-m,e2m-m]内有两个实根。
 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
设i是虚数单位,复数z和w满足zw+2iz-2iw+1=0
(1)若z和w又满足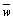 -z=2i,求z和w值。
-z=2i,求z和w值。
(2)求证:如果|z|=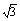 ,那么|w-4i|的值是一
,那么|w-4i|的值是一 个常数,并求这个常数。
个常数,并求这个常数。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)在x=1处的导数为3,f(x)的解析式可能为 ( )
A.f(x)=(x-1 )3+32(x-1) B.f(x)=2x+1
)3+32(x-1) B.f(x)=2x+1
C.f()=2(x-1)2 D.f(x)-x+3
查看答案和解析>>
科目:高中数学 来源: 题型:
某学生在体育训练时弄伤了膝关节,医生给开了一些消炎药,并嘱咐每天早晚8点各服用一片药片,已知该药品 每征220m
每征220m g,他的贤脏每次12小时从体内滤出这种药的60%,如果这种药在体内残留超过386mg,将产生副作用。
g,他的贤脏每次12小时从体内滤出这种药的60%,如果这种药在体内残留超过386mg,将产生副作用。
请问:(1)该同学上午8时第一次服药后,到第二天早晨服药后,药在体内还残留多少?
(2)该同学若长期服用该药,会不会产生副作用?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com