
分析 (Ⅰ)由题意可得 f(x),分类讨论求得不等式f(x)>4的解集P.
(Ⅱ)由题意可得m2≥4,n2≥4,计算左边的平方减去右边的平方的结果大于或等于零,不等式得证.
解答 (Ⅰ)解:f(x)=|x-1|+|x+1|=$\left\{\begin{array}{l}{2x,x≥1}\\{2,-1<x<1}\\{-2x,x≤-1}\end{array}\right.$,
由f(x)的单调性及f(x)>4得,$\left\{\begin{array}{l}{2x>4}\\{x≥1}\end{array}\right.$或$\left\{\begin{array}{l}{-2x>4}\\{x≤-1}\end{array}\right.$,解得x>2或x<-2.
所以不等式f(x)>4的解集为P={x|x>2或x<-2}.
(Ⅱ)证明:由(Ⅰ)可知|m|>2,|n|>2,
所以m2>4,n2>4,(mn+4)2-4(m+n)2=(m2-4)(n2-4)>0,
所以(mn+4)2>4(m+n)2,
从而有|mn+4|>2|m+n|.
点评 本题主要考查绝对值不等式的解法,体现了等价转化和分类讨论的数学思想,用比较法证明不等式,属于中档题.


科目:高中数学 来源: 题型:解答题
| 年份序号x | 1 | 2 | 3 | 4 | 5 |
| 录取人数y | 10 | 11 | 14 | 16 | 19 |
| 接受超常实验班教育 | 未接受超常实验班教育 | 合计 | |
| 录取少年大学生 | 60 | 20 | 80 |
| 未录取少年大学生 | 10 | 10 | 20 |
| 合计 | 70 | 30 | 100 |
| P(k2≥k0) | 0.50 | 0.40 | 0.10 | 0.05 |
| k0 | 0.455 | 0.708 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
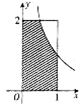 如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数$y=\frac{1}{x}(x>0)$图象下方的阴影部分区域,则阴影部分E的面积为1+ln2.
如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数$y=\frac{1}{x}(x>0)$图象下方的阴影部分区域,则阴影部分E的面积为1+ln2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com