
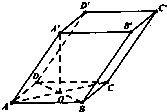
 如图四棱柱ABCD-A′B′C′D′的底面是正方形,O是底面的中心,A′O=1,AB=AA′=A′D=A′B=
如图四棱柱ABCD-A′B′C′D′的底面是正方形,O是底面的中心,A′O=1,AB=AA′=A′D=A′B=| 2 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |


科目:高中数学 来源: 题型:
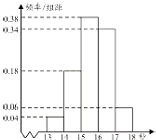 高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:
| 合格品 | 次品 | 总计 | |
| 第一台车床加工的零件数 | 35 | 5 | 40 |
| 第二台车床加工的零件数 | 50 | 10 | 60 |
| 总计 | 85 | 15 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,多面体ABCDEFG中,四边形ABCD,CDEF都是边长为2的正方形,DE⊥平面ABCD,AG⊥平面ABCD,且AG=1.
如图,多面体ABCDEFG中,四边形ABCD,CDEF都是边长为2的正方形,DE⊥平面ABCD,AG⊥平面ABCD,且AG=1.查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
| ||
| 5 |
| QF2 |
| PF2 |
| 11 |
| 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com