
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,四边形ABCD是正方形,CD=PD,∠ADP=90°,∠CDP=120°,E,F,G分别为PB,BBC,AP的中点.
如图,在四棱锥P-ABCD中,四边形ABCD是正方形,CD=PD,∠ADP=90°,∠CDP=120°,E,F,G分别为PB,BBC,AP的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 某校举行演讲比赛,9位评委给选手A打出的分数如茎叶图所示,统计员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若统计员计算无误,则数字x应该是
某校举行演讲比赛,9位评委给选手A打出的分数如茎叶图所示,统计员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若统计员计算无误,则数字x应该是查看答案和解析>>
科目:高中数学 来源: 题型:
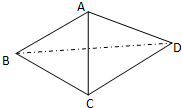 如图所示的三棱锥A-BCD中,∠BAD=90°,AD⊥BC,AD=4,AB=AC=2
如图所示的三棱锥A-BCD中,∠BAD=90°,AD⊥BC,AD=4,AB=AC=2| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com