
分析 (Ⅰ)求出f(x)的导数,根据函数的单调性求出函数的单调区间即可;
(Ⅱ)①构造函数φ(x),根据函数的单调性证明即可;
②结合①求出0<lnx•ln(1-x)<$\sqrt{x(1-x)}$,结合不等式的性质判断即可.
解答 解:(Ⅰ)函数的定义域为(0,1),由于f(1-x)=f(x),
故只需要考虑$x∈(0,\frac{1}{2})$的单调性 (1分)
$f'(x)=\frac{ln(1-x)}{x}-\frac{lnx}{1-x}=\frac{1}{1-x}[{\frac{1-x}{x}ln(1-x)-lnx}]$(2分)
令$g(x)=\frac{1-x}{x}ln(1-x)-lnx$则$g'(x)=-\frac{ln(1-x)+2x}{x^2}$(3分)
再令h(x)=ln(1-x)+2x则$h'(x)=2-\frac{1}{1-x}=\frac{1-2x}{1-x}$(4分)
当$x∈(0,\frac{1}{2})$时,h'(x)>0,则h(x)单调递增,又h(0)=0,∴h(x)>h(0)=0
则g'(x)<0∴g(x)单调递减∴$g(x)>g(\frac{1}{2})=0$∴f'(x)>0
∴f(x)的单调递增区间为$(0,\frac{1}{2})$,单调递减区间为$(\frac{1}{2},1)$(6分)
(Ⅱ)①令$φ(x)=lnx-\frac{x-1}{{\sqrt{x}}}=lnx-\sqrt{x}+\frac{1}{{\sqrt{x}}}(0<x<1)$,
$φ'(x)=\frac{1}{x}-\frac{1}{{2\sqrt{x}}}-\frac{1}{{2x\sqrt{x}}}=\frac{{-{{(\sqrt{x}-1)}^2}}}{{2x\sqrt{x}}}<0$
则φ(x)在(0,1)单调递减,
∴φ(x)>φ(1)=0即$lnx>\frac{x-1}{{\sqrt{x}}}$(9分)
②由①得$-lnx<\frac{1-x}{{\sqrt{x}}}⇒-ln(1-x)<\frac{x}{{\sqrt{1-x}}}$
∴$0<(lnx)ln(1-x)<\sqrt{x(1-x)}$
∴${(x-\frac{1}{2})^2}+{y^2}={(x-\frac{1}{2})^2}+{[{(lnx)ln(1-x)}]^2}<{(x-\frac{1}{2})^2}+x(1-x)=\frac{1}{4}$,
故曲线y=f(x)上的所有点都落在圆$C:{(x-\frac{1}{2})^2}+{y^2}=\frac{1}{4}$内. (12分)
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及转化思想,不等式的性质,是一道中档题.


科目:高中数学 来源: 题型:解答题
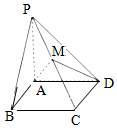 已知四棱锥P-ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC上一点,M为PC的中点.
已知四棱锥P-ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC上一点,M为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 40 | C. | 60 | D. | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 份(x) | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 |
| 水上狂欢节届编号x | 1 | 2 | 3 | 4 | 5 |
| 外地游客人数y(单位:十万) | 0.6 | 0.8 | 0.9 | 1.2 | 1.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com