Question

14．已知函数f（x）=3sin（$\frac{x}{2}$+$\frac{π}{6}$）+3
（1）用五点法画出它在一个周期内的闭区间上的图象；

（2）指出f（x）的周期、振幅、初相、对称轴；
（3）求此函数的最大值、最小值及相对应自变量x的集合；
（4）说明此函数图象可由y=sinx的图象经怎样的变换得到．

Answer 1

分析 （1）利用五点法，可得函数的图象；
（2）利用函数解析式可知周期、振幅、初相、对称轴；
（3）利用函数的图象，可得f（x）最值及x的集合．
（4）利用三角函数图象变换规律，可得结论

解答 解：（1）列表如下：

x	$-\frac{π}{3}$	$\frac{2π}{3}$	$\frac{5π}{3}$	$\frac{8π}{3}$	$\frac{11π}{3}$
$\frac{x}{2}+\frac{π}{6}$	0	$\frac{π}{2}$	π	$\frac{3π}{2}$	2π
y	3	6	3	0	3

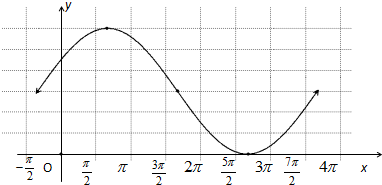…（5分）；
（2）∴其周期T=$\frac{2π}{\frac{1}{2}}=4π$，振幅A=3，初相φ=$\frac{π}{6}$，由（$\frac{x}{2}$+$\frac{π}{6}$）=kπ+$\frac{π}{2}$（k∈Z），得x=2kπ+$\frac{2π}{3}$（k∈Z）即为对称轴
（3）当sin（$\frac{x}{2}$+$\frac{π}{6}$）=1时函数的最大值为3+3=6，此时（$\frac{x}{2}$+$\frac{π}{6}$）=2kπ+$\frac{π}{2}$（k∈Z），解得x的集合为{x|x=4kπ+$\frac{2π}{3}$，k∈Z}；
当sin（$\frac{x}{2}$+$\frac{π}{6}$）=-1时，函数的最小值为-3+3=0；此时（$\frac{x}{2}$+$\frac{π}{6}$）=2kπ-$\frac{π}{2}$（k∈Z），解得x 的集合为{x|x=4kπ-$\frac{4π}{3}$，k∈Z}…（8分）；
（4）①由y=sinx的图象上各点向左平移ϕ=$\frac{π}{6}$个长度单位，得y=sin（x+$\frac{π}{6}$）的图象；
②由y=sin（x+$\frac{π}{6}$）的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），得y=sin（$\frac{x}{2}$+$\frac{π}{6}$）的图象；
③由y=3sin（$\frac{x}{2}$+$\frac{π}{6}$）的图象上各点的纵坐标伸长为原来的3倍（横坐标不变），得y=3sin（$\frac{x}{2}$+$\frac{π}{6}$）的图象；
④由y=3sin（$\frac{x}{2}$+$\frac{π}{6}$）的图象上各点向上平移3个长度单位，得y=3sin（$\frac{x}{2}$+$\frac{π}{6}$）+3的图象．

点评 本题考查用五点法作图，着重考查正弦函数的性质与作图能力，考查三角函数的图象与性质，考查学生分析解决问题的能力，属于中档题．