
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
���� �ɸ���$y=x+\frac{1}{x}��y=x+\frac{2}{x}��y=x+\frac{3}{x}$�ڣ�0��+�ޣ��ϵĵ����ԣ��Ӷ����Ƶ�������$y=x+\frac{{3}^{m}}{x}$�ڣ�0��+�ޣ��ϵĵ����ԣ�����������ú�������Сֵ������СֵΪ6���ɽ�������m�ķ��̣��ⷽ�̱�ɵó�m��ֵ��
��� �⣺�������ã�
$y=x+\frac{{3}^{m}}{x}$�ڣ�0��$\sqrt{{3}^{m}}$]���Ǽ���������$[\sqrt{{3}^{m}}��+�ޣ�$������������
��$x=\sqrt{{3}^{m}}$ʱ���ú����ڣ�0��+�ޣ���ȡ��Сֵ$\sqrt{{3}^{m}}+\frac{{3}^{m}}{\sqrt{{3}^{m}}}=2\sqrt{{3}^{m}}=6$��
��3m=9��
��m=2��
��ѡB��
���� ����Ժ���$y=x+\frac{1}{x}��y=x+\frac{2}{x}$�Լ�$y=x+\frac{3}{x}$�����Ե��жϣ��Ӷ���ͨ�����ɵķ����ó�����$y=x+\frac{a}{x}$��a��0���ĵ����ԣ������ܹ��ó�$y=x+\frac{{3}^{m}}{x}$�ĵ����ԣ��Լ����ݵ�����������ֵ�ķ�����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
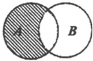
| A�� | {1��2��3��4} | B�� | {1��2��3} | C�� | {4��5} | D�� | {1��4} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | E��F=∅ | B�� | E��F=R | C�� | E⊆F | D�� | F⊆E |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | h��x��=f��x��+g��x����ż���� | B�� | h��x��=f��x��•g��x�����溯�� | ||
| C�� | h��x��=$\frac{g��x��•f��x��}{2-x}$��ż���� | D�� | h��x��=$\frac{f��x��}{2-g��x��}$���溯�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com