Question

11．如图，四棱柱ABCD-A₁B₁C₁D₁的底面ABCD是菱形，AC∩BD=O，A₁O⊥底面ABCD，AB=AA₁=2．
（Ⅰ）证明：BD⊥平面A₁CO；
（Ⅱ）若∠BAD=60°，求点C到平面OBB₁的距离．

Answer 1

分析 （Ⅰ）证明A₁O⊥BD．CO⊥BD．即可证明BD⊥平面A₁CO．
（Ⅱ）解法一：说明点B₁到平面ABCD的距离等于点A₁到平面ABCD的距离A₁O．设点C到平面OBB₁的距离为d，
通过${V_{C-OB{B_1}}}={V_{{B_1}-OBC}}$，求解点C到平面OBB₁的距离．
解法二：连接A₁C₁与B₁D₁交于点O₁，连接CO₁，OO₁，推出OA₁O₁C为平行四边形．证明CH⊥平面BB₁D₁D，然后求解点C到平面OBB₁的距离．

解答 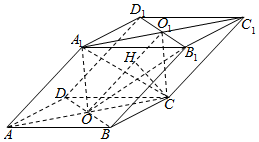（Ⅰ）证明：因为A₁O⊥平面ABCD，BD?平面ABCD，
所以A₁O⊥BD．…（1分）
因为ABCD是菱形，所以CO⊥BD．…（2分）
因为A₁O∩CO=O，A₁O，CO?平面A₁CO，
所以BD⊥平面A₁CO．…（3分）
（Ⅱ）解法一：因为底面ABCD是菱形，AC∩BD=O，AB=AA₁=2，∠BAD=60°，
所以OB=OD=1，$OA=OC=\sqrt{3}$．…（4分）
所以△OBC的面积为${S_{△OBC}}=\frac{1}{2}×OB×OC=\frac{1}{2}×1×\sqrt{3}=\frac{{\sqrt{3}}}{2}$．…（5分）
因为A₁O⊥平面ABCD，AO?平面ABCD，
所以A₁O⊥AO，${A_1}O=\sqrt{A{A_1}^2-O{A^2}}=1$．…（6分）
因为A₁B₁∥平面ABCD，
所以点B₁到平面ABCD的距离等于点A₁到平面ABCD的距离A₁O．…（7分）
由（Ⅰ）得，BD⊥平面A₁AC．
因为A₁A?平面A₁AC，所以BD⊥A₁A．
因为A₁A∥B₁B，所以BD⊥B₁B．…（8分）
所以△OBB₁的面积为${S_{△OB{B_1}}}=\frac{1}{2}×OB×B{B_1}=\frac{1}{2}×1×2=1$．…（9分）
设点C到平面OBB₁的距离为d，
因为${V_{C-OB{B_1}}}={V_{{B_1}-OBC}}$，
所以$\frac{1}{3}{S_{△OB{B_1}}}•d=\frac{1}{3}{S_{△OBC}}•{A_1}O$．…（10分）
所以$d=\frac{{{S_{△OBC}}•{A_1}O}}{{{S_{△OB{B_1}}}}}=\frac{{\frac{{\sqrt{3}}}{2}×1}}{1}=\frac{{\sqrt{3}}}{2}$．
所以点C到平面OBB₁的距离为$\frac{{\sqrt{3}}}{2}$．…（12分）
解法二：由（Ⅰ）知BD⊥平面A₁CO，
因为BD?平面BB₁D₁D，
所以平面A₁CO⊥平面BB₁D₁D．…（4分）
连接A₁C₁与B₁D₁交于点O₁，
连接CO₁，OO₁，
因为AA₁=CC₁，AA₁∥CC₁，所以CAA₁C₁为平行四边形．
又O，O₁分别是AC，A₁C₁的中点，所以OA₁O₁C为平行四边形．
所以O₁C=OA₁=1．…（6分）
因为平面OA₁O₁C与平面BB₁D₁D交线为OO₁，
过点C作CH⊥OO₁于H，则CH⊥平面BB₁D₁D．…（8分）
因为O₁C∥A₁O，A₁O⊥平面ABCD，所以O₁C⊥平面ABCD．
因为OC?平面ABCD，所以O_•1C⊥OC，即△OCO₁为直角三角形．…（10分）
所以$CH=\frac{{{O_1}C•OC}}{{O{O_1}}}=\frac{{1×\sqrt{3}}}{2}=\frac{{\sqrt{3}}}{2}$．
所以点C到平面OBB₁的距离为$\frac{{\sqrt{3}}}{2}$．…（12分）

点评 本题考查空间想象能力以及计算能力，考查直线与平面垂直的判定定理以及点线面距离的求法，考查转化思想．