
| lim |
| x→1 |
| x-1 |
| x2+ax+b |
| 1 |
| 4 |
| A、-6 | B、-5 | C、5 | D、6 |
科目:高中数学 来源: 题型:
 如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在以点C为圆心,且与直线BD相切的圆内运动,设
如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在以点C为圆心,且与直线BD相切的圆内运动,设| AP |
| AD |
| AB |
A、(0,
| ||||
B、[
| ||||
C、(1,
| ||||
D、(1,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
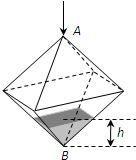 如图所示,连结棱长为2cm的正方体各面的中心得一个多面体容器,从顶点A处向该容器内注水,注满为止.已知顶点B到水面的高度h以每秒1cm匀速上升,记该容器内水的体积V(cm3)与时间T(S)的函数关系是V(t),则函数V(t)的导函数y=V′(t)的图象大致是( )
如图所示,连结棱长为2cm的正方体各面的中心得一个多面体容器,从顶点A处向该容器内注水,注满为止.已知顶点B到水面的高度h以每秒1cm匀速上升,记该容器内水的体积V(cm3)与时间T(S)的函数关系是V(t),则函数V(t)的导函数y=V′(t)的图象大致是( )A、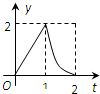 |
B、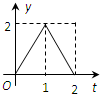 |
C、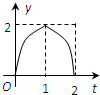 |
D、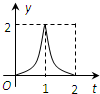 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出五个结论:①OM∥PD;②OM∥平面PCD;③OM∥平面PDA;④OM∥平面PBA,⑤OM∥平面PCB.
P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出五个结论:①OM∥PD;②OM∥平面PCD;③OM∥平面PDA;④OM∥平面PBA,⑤OM∥平面PCB.| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AD |
| BC |
| A、[1,2] |
| B、[0,1] |
| C、[0,2] |
| D、[-5,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图1所示,在边长为12的正方形ADD1A1中,点B,C在线段AD上,且AB=3,BC=4,作BB1∥AA1,分别交A1D1,AD1于点B1,P,作CC1∥AA1,分别交A1D1,AD1于点C1,Q,将该正方形沿BB1,CC1折叠,使得DD1与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.
如图1所示,在边长为12的正方形ADD1A1中,点B,C在线段AD上,且AB=3,BC=4,作BB1∥AA1,分别交A1D1,AD1于点B1,P,作CC1∥AA1,分别交A1D1,AD1于点C1,Q,将该正方形沿BB1,CC1折叠,使得DD1与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.
| ||
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com