练习册

  • 练习册
  • 试题
    相关习题
     0  230323  230331  230337  230341  230347  230349  230353  230359  230361  230367  230373  230377  230379  230383  230389  230391  230397  230401  230403  230407  230409  230413  230415  230417  230418  230419  230421  230422  230423  230425  230427  230431  230433  230437  230439  230443  230449  230451  230457  230461  230463  230467  230473  230479  230481  230487  230491  230493  230499  230503  230509  230517  266669 

    科目： 来源： 题型：解答题

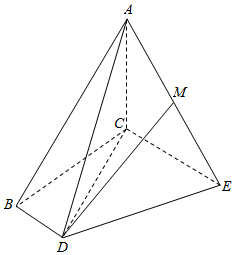    18．如图所示，△ABC是边长为2的正三角形，EC⊥平面ABC，DB⊥平面ABC，且M为AE的中点，CE=CA=2BD．
    （1）求证：DM∥平面ABC；
    （2）求证：平面DEA⊥平面ECA；
    （3）求点E到平面ACD的距离．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    17．已知数列{an}是各项均为正数的等比数列，a1=1，5（a1+a2）=a1+a2+a3+a4，
    （1）求{an}的通项公式及前n项和Sn；
    （2）设Tn=$\frac{{a}_{1}}{{S}_{1}{S}_{2}}$+$\frac{{a}_{2}}{{S}_{2}{S}_{3}}$+…+$\frac{{a}_{n}}{{S}_{n}{S}_{n+1}}$，求证：Tn＜$\frac{1}{2}$．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    16．已知函数f（x）=|x+1|+|x-a|．
    （Ⅰ）当a=2时，若函数f（x）为常函数，求x的取值范围．
    （Ⅱ）若不等式2f（x）-2|x+1|+x+3a-1＞0对x∈R恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    15．移动公司为了了解4G用户的使用情况，随机抽取了60名男手机用户，50名女手机用户，统计数据如表所示，试确定是否为4G用户与性别有关的把握约为（　　）
    使用4G未使用4G总计
    男用户402060
    女用户203050
    总计6050110
    附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，n=a+b+c+d．
    P（ K2≥k0）0.5000.1000.0500.0100.001
    k00，4552，7063.8416.63510.828
    A．90%B．95%C．99%D．99.9%

    查看答案和解析>>

    科目： 来源： 题型：解答题

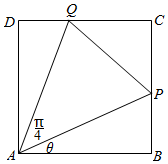    14．如图，某房产开发商计划在一正方形土地ABCD内建造一个三角形住宅区，在其余土地种植绿化，住宅区形状为三角形APQ，其中P位于边CB上，Q位于边CD上．已知，∠PAQ=$\frac{π}{4}$，设∠PAB=θ，记绿化率L=1-$\frac{△PAQ面积}{正方形ABCD面积}$，若L越大，则住宅区绿化越好．
    （1）求L（θ）关于θ的函数解析式；
    （2）问当θ取何值时，L有最大值？并求出L的最大值．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    13．某三棱柱被一个平面截去一部分后所得的几何体的三视图如图所示，其中俯视图是边长为2的正三角形，则截去部分和剩余部分的体积之比为（　　）
    A．$\frac{10}{33}$B．$\frac{13}{36}$C．$\frac{13}{23}$D．$\frac{23}{33}$

    查看答案和解析>>

    科目： 来源： 题型：解答题

    12．已知函数f（x）=sinωx（sinωx+$\sqrt{3}$cosωx），（ω＞0）且函数y=f（x）的最小正周期为π．
    （1）求f（$\frac{π}{12}$）的值；
    （2）求函数y=f（x+$\frac{π}{12}$）在区间[-$\frac{π}{6}$，$\frac{π}{3}$]上的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    11．直角坐标系xOy平面内，已知动点M到点D（-4，0）与E（-1，0）的距离之比为2．
    （Ⅰ）求动点M的轨迹C的方程；
    （Ⅱ）是否存在经过点（-1，1）的直线l，它与曲线C相交于A，B两个不同点，且满足$\overrightarrow{OM}$=$\frac{1}{2}\overrightarrow{OA}$+$\frac{{\sqrt{3}}}{2}\overrightarrow{OB}$（O为坐标原点）关系的点M也在曲线C上，如果存在，求出直线l的方程；如果不存在，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：解答题

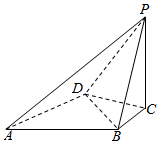    10．如图，在四棱锥P-ABCD中，△ABD是边长为2的正三角形，PC⊥底面ABCD，AB⊥BP，BC=$\frac{2\sqrt{3}}{3}$．
    （1）求证：PA⊥BD；
    （2）若PC=BC，求二面角A-BP-D的正弦值．

    查看答案和解析>>

    科目： 来源： 题型：填空题

    9．一个几何体的三视图如图所示（单位cm），则该几何体的体积为6$\sqrt{3}$+$\frac{2π}{3}$cm3．

    查看答案和解析>>

    同步练习册答案