
科目: 来源: 题型:
【题目】为了解高中生上学使用手机情况,调查者进行了如下的随机调查:调查者向被调查者提出两个问题:(1)你的学号是奇数吗?(2)你上学时是否经常带手机?要求被调查者背对着调查人员抛掷一枚硬币,如果出现正面,就回答第一问题,否则就回答第二个问题.被调查者不必告诉调查人员自己回答的是哪一个问题,只需回答“是”或“不是”,因为只有被调查者本人知道回答了哪一个问题,所以都如实地做了回答.结果被调查的800人(学号从1至800)中有260人回答了“是”.由此可以估计这800人中经常带手机上学的人数是_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】(A)已知平行四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() .
.
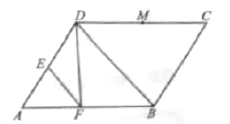
(1)求![]() 的长;
的长;
(2)设![]() ,
, ![]() 为线段
为线段![]() 、
、![]() 上的动点,且
上的动点,且![]() ,求
,求![]() 的最小值.
的最小值.
(B)已知平行四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() .
.
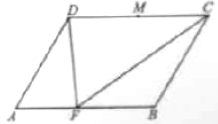
(1)求![]() 的长;
的长;
(2)设![]() 为线段
为线段![]() 上的动点(不包含端点),求
上的动点(不包含端点),求![]() 的最小值,以及此时点
的最小值,以及此时点![]() 的位置.
的位置.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图(a),在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=8,AD=CD=4,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图(b)所示.

(1)求证:BC⊥平面ACD;
(2)求几何体D-ABC的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某网络营销部门为了统计某市网友“双11”在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如图):

若网购金额超过2千元的顾客定义为“网购达人”,网购金额不超过2千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为3:2.
(1)试确定![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)试营销部门为了进一步了解这60名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定5人,若需从这5人中随机选取2人进行问卷调查,则恰好选取1名“网购达人”和1名“非网购达人”的概率是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】(A)已知![]() ,
, ![]() ,
, ![]() ,且函数
,且函数![]() 的最小正周期为
的最小正周期为![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,
, ![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的值.
的值.
(B)已知![]() ,
, ![]() ,
, ![]() ,且函数
,且函数![]() 的最小正周期为
的最小正周期为![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若关于![]() 的方程
的方程![]() ,在
,在![]() 内有两个不同的解
内有两个不同的解![]() ,
, ![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法不正确的是( )
A. ![]() ,
, ![]() 为不共线向量,若
为不共线向量,若![]() ,则
,则![]()
B. 若![]() ,
, ![]() 为平面内两个不相等向量,则平面内任意向量
为平面内两个不相等向量,则平面内任意向量![]() 都可以表示为
都可以表示为![]()
C. 若![]() ,
, ![]() ,则
,则![]() 与
与![]() 不一定共线
不一定共线
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线l:![]() 与圆O:
与圆O:![]() 相交于A,B两个不同的点,且A
相交于A,B两个不同的点,且A![]() ,B
,B![]() .
.
(1)当![]() 面积最大时,求m的取值,并求出
面积最大时,求m的取值,并求出![]() 的长度.
的长度.
(2)判断![]() 是否为定值;若是,求出定值的大小;若不是,说明理由.
是否为定值;若是,求出定值的大小;若不是,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 的左焦点
的左焦点![]() 在直线
在直线![]() 上.
上.
(1)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com