
科目: 来源: 题型:
【题目】近年来,随着我国汽车消费水平的提高,二手车流通行业得到迅猛发展.某汽车交易市场对2017年成交的二手车交易前的使用时间(以下简称“使用时间”)进行统计,得到频率分布直方图如图1.


图1 图2
(1)记“在![]() 年成交的二手车中随机选取一辆,该车的使用年限在
年成交的二手车中随机选取一辆,该车的使用年限在![]() ”为事件
”为事件![]() ,试估计
,试估计![]() 的概率;
的概率;
(2)根据该汽车交易市场的历史资料,得到散点图如图2,其中![]() (单位:年)表示二手车的使用时间,
(单位:年)表示二手车的使用时间,![]() (单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用
(单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用![]() 作为二手车平均交易价格
作为二手车平均交易价格![]() 关于其使用年限
关于其使用年限![]() 的回归方程,相关数据如下表(表中
的回归方程,相关数据如下表(表中![]() ,
,![]() ):
):

①根据回归方程类型及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
②该汽车交易市场对使用8年以内(含8年)的二手车收取成交价格![]() 的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格
的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格![]() 的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
附注:①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;
②参考数据:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某跳水运动员在一次跳水训练时的跳水曲线为如图所示抛物线的一段.已知跳水板![]() 长为
长为![]() ,跳水板距水面
,跳水板距水面![]() 的高
的高![]() 为
为![]() .为安全和空中姿态优美,训练时跳水曲线应在离起跳点
.为安全和空中姿态优美,训练时跳水曲线应在离起跳点![]() 处水平距
处水平距![]()
![]() 时达到距水面最大高度
时达到距水面最大高度![]() ,规定:以
,规定:以![]() 为横轴,
为横轴,![]() 为纵轴建立直角坐标系.
为纵轴建立直角坐标系.
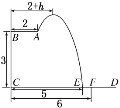
(1)当![]() 时,求跳水曲线所在的抛物线方程;
时,求跳水曲线所在的抛物线方程;
(2)若跳水运动员在区域![]() 内入水时才能达到比较好的训练效果,求此时
内入水时才能达到比较好的训练效果,求此时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C: ![]() (a>0,b>0)的离心率为
(a>0,b>0)的离心率为 ![]() ,点A(0,﹣2)与椭圆右焦点F的连线的斜率为
,点A(0,﹣2)与椭圆右焦点F的连线的斜率为 ![]() .
.
(1)求椭圆C的方程;
(2)O为坐标原点,过点A的直线l与椭圆C相交于P,Q两点,当△OPQ的面积最大时,求直线l的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上. 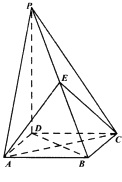
(1)求证:平面AEC⊥平面PDB;
(2)当PD=2AB,且E为PB的中点,求二面角B﹣AE﹣C的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)为二次函数,且f(x-1)+f(x)=2x2+4.
(1)求f(x)的解析式;
(2)当x∈[t,t+2],t∈R时,求函数f(x)的最小值(用t表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】通过随机询问100性别不同的大学生是否爱好某项运动,得到如下2×2列联表:
男 | 女 | 总计 | |
爱好 | 40 | ||
不爱好 | 25 | ||
总计 | 45 | 100 |
(1)将题中的2×2列联表补充完整;
(2)能否有99%的把握认为断爱好该项运动与性别有关?请说明理由;
附:K2= ![]() ,
,
p(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
(3)利用分层抽样的方法从以上爱好该项运动的大学生中抽取6人组建了“运动达人社”,现从“运动达人设”中选派3人参加某项校际挑战赛,记选出3人中的女大学生人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知正四棱柱ABCD﹣A1B1C1D1(底面是正方形,侧棱垂直于底面)的8个顶点都在球O的表面上,AB=1,AA1′=2,则球O的半径R=;若E,F是棱AA1和DD1的中点,则直线EF被球O截得的线段长为 . 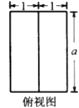
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定义在R上的函数f(x)满足f(﹣x)=f(x),且当x<0,f(x)=3x+1,若a= ![]() ,b=
,b= ![]() ,c=2
,c=2 ![]() ,则有( )
,则有( )
A.f(a)<f(b)<f(c)
B.f(b)<f(c)<f(a)
C.f(b)<f(a)<f(c)
D.f(c)<f(a)<f(b)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com