
科目: 来源: 题型:
【题目】为了解某地区中学生的身体发育状况,拟采用分层抽样的方法从甲、乙、丙三所中学抽取![]() 个教学班进行调查.已知甲、乙、丙三所中学分别有
个教学班进行调查.已知甲、乙、丙三所中学分别有![]() ,
, ![]() ,
, ![]() 个教学班.
个教学班.
(Ⅰ)求从甲、乙、丙三所中学中分别抽取的教学班的个数.
(Ⅱ)若从抽取的![]() 个教学班中随机抽取
个教学班中随机抽取![]() 个进行调查结果的对比,求这
个进行调查结果的对比,求这![]() 个教学班中至少有一个来自甲学校的概率.
个教学班中至少有一个来自甲学校的概率.
查看答案和解析>>
科目: 来源: 题型:
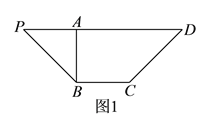
【题目】如图![]() ,等腰梯形
,等腰梯形![]() 中,
中, ![]() ,
, ![]() 于点
于点![]() ,
, ![]() ,且
,且![]() .沿
.沿![]() 把
把![]() 折起到
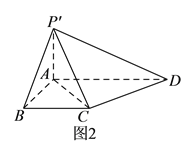
折起到![]() 的位置(如图
的位置(如图![]() ),使
),使![]() .
.
(I)求证: ![]() 平面
平面![]() .
.
(II)求三棱锥![]() 的体积.
的体积.
(III)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,指出点
,若存在,指出点![]() 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 是由正整数组成的无穷数列,该数列前
是由正整数组成的无穷数列,该数列前![]() 项的最大值记为
项的最大值记为![]() ,第
,第![]() 项之后各项
项之后各项![]() ,
, ![]() ,
, ![]() 的最小值记为
的最小值记为![]() ,
, ![]() .
.
(I)若![]() 为
为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,是一个周期为
,是一个周期为![]() 的数列(即对任意
的数列(即对任意![]() ,
, ![]() ),写出
),写出![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值.
的值.
(II)设![]() 是正整数,证明:
是正整数,证明: ![]() 的充分必要条件为
的充分必要条件为![]() 是公比为
是公比为![]() 的等比数列.
的等比数列.
(III)证明:若![]() ,
, ![]() ,则
,则![]() 的项只能是
的项只能是![]() 或者
或者![]() ,且有无穷多项为
,且有无穷多项为![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .直角梯形
.直角梯形![]() 可以通过直角梯形
可以通过直角梯形![]() 以直线
以直线![]() 为轴旋转得到,且平面
为轴旋转得到,且平面![]() 平面
平面![]() .
.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2017/12/20/1842736631291904/1845869604462592/STEM/592e486e595e40bf846fae2bfa16ac59.png]
(I)求证: ![]() .
.
(II)求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
(III)设![]() 为
为![]() 的中点,
的中点, ![]() ,
, ![]() 分别为线段
分别为线段![]() ,
, ![]() 上的点(都不与点
上的点(都不与点![]() 重合).若直线
重合).若直线![]() 平面
平面![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某花店每天以每枝![]() 元的价格从农场购进若干枝玫瑰花,然后以每枝
元的价格从农场购进若干枝玫瑰花,然后以每枝![]() 元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(I)若花店一天购进![]() 枝玫瑰花,写出当天的利润
枝玫瑰花,写出当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝, ![]() )的函数解析式.
)的函数解析式.
(II)花店记录了![]() 天玫瑰花的日需求量(单位:枝),整理得下表:
天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
以![]() 天记录的各需求量的频率作为各需求量发生的概率.
天记录的各需求量的频率作为各需求量发生的概率.
(i)若花店一天购进![]() 枝玫瑰花,
枝玫瑰花, ![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列,数学期望.
的分布列,数学期望.
(ii)若花店计划一天购进![]() 枝或
枝或![]() 枝玫瑰花,你认为应购进
枝玫瑰花,你认为应购进![]() 枝还是
枝还是![]() 枝?只写结论.
枝?只写结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线l过点P(-3,2),倾斜角为![]() ,且
,且![]() .曲线C的参数方程为
.曲线C的参数方程为![]() (
(![]() 为参数).直线l与曲线C交于A、B两点,线段AB的中点为M.
为参数).直线l与曲线C交于A、B两点,线段AB的中点为M.
(Ⅰ)求直线l的参数方程和曲线C的普通方程;
(Ⅱ)求线段PM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com