
科目: 来源: 题型:
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为棱
为棱![]() 上一点,
上一点,![]() .
.

(1)确定![]() 的位置,使得平面
的位置,使得平面![]()
![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(2)设二面角![]() 的正切值为
的正切值为![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,且
上一点,且![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() 是直线
是直线![]() 上的
上的![]() 个不同的点(
个不同的点(![]() ,
,![]() 、
、![]() ,均为非零常数),其中数列
,均为非零常数),其中数列![]() 为等差数列.
为等差数列.![]()
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)若点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求证:
,求证:![]() ;
;
(3)设![]() ,且当
,且当![]() 时,恒有
时,恒有![]() (
(![]() 和
和![]() 都是不大于
都是不大于![]() 的正整数,且
的正整数,且![]() )试探索:若
)试探索:若![]() 为直角坐标原点,在直线
为直角坐标原点,在直线![]() 上是否存在这样的点
上是否存在这样的点![]() ,使得
,使得![]() 成立?请说明你的理由.
成立?请说明你的理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到表(单位:人)
经常网购 | 偶尔或不用网购 | 合计 | |
男性 | 50 | 100 | |
女性 | 70 | 100 | |
合计 |
(1)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关?
(2)①现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
②将频率视为概率,从我市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为![]() ,求随机变量
,求随机变量![]() 的数学期望和方差.
的数学期望和方差.
参考公式: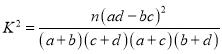
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】从某小区抽取50户居民进行月用电量调查,发现其用电量都在50到350度之间,将用电量的数据绘制成频率分布直方图如下.

(1)求频率分布直方图中![]() 的值并估计这50户用户的平均用电量;
的值并估计这50户用户的平均用电量;
(2)若将用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为低用电家庭,用电量在区间
类用户,标记为低用电家庭,用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
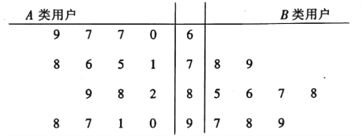
①从![]() 类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
②若打分超过85分视为满意,没超过85分视为不满意,请填写下面列联表,并根据列联表判断是否有![]() 的把握认为“满意度与用电量高低有关”?
的把握认为“满意度与用电量高低有关”?
满意 | 不满意 | 合计 | |
| |||
| |||
合计 |
附表及公式:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
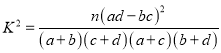 ,
, ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 交于点
交于点![]() ,曲线
,曲线![]() 与
与![]() 轴交于点
轴交于点![]() ,求线段
,求线段![]() 的中点到点
的中点到点![]() 的距离.
的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】“克拉茨猜想”又称“![]() 猜想”,是德国数学家洛萨克拉茨在1950年世界数学家大会上公布的一个猜想:任给一个正整数
猜想”,是德国数学家洛萨克拉茨在1950年世界数学家大会上公布的一个猜想:任给一个正整数![]() ,如果
,如果![]() 是偶数,就将它减半;如果
是偶数,就将它减半;如果![]() 为奇数就将它乘3加1,不断重复这样的运算,经过有限步后,最终都能够得到1.己知正整数
为奇数就将它乘3加1,不断重复这样的运算,经过有限步后,最终都能够得到1.己知正整数![]() 经过6次运算后得到1,则
经过6次运算后得到1,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() (
(![]() 为常数,且
为常数,且![]() ).
).
(1)若当![]() 时,函数
时,函数![]() 与
与![]() 的图象有且只要一个交点,试确定自然数
的图象有且只要一个交点,试确定自然数![]() 的值,使得
的值,使得![]() (参考数值
(参考数值![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)当![]() 时,证明:
时,证明:![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
查看答案和解析>>
科目: 来源: 题型:
【题目】朱世杰是历史上最伟大的数学家之一,他所著的![]() 四元玉鉴
四元玉鉴![]() 卷中“如像招数”五问有如下问题:“今有官司差夫一千八百六十四人筑堤
卷中“如像招数”五问有如下问题:“今有官司差夫一千八百六十四人筑堤![]() 只云初日差六十四人,次日转多七人,每人日支米三升,共支米四百三石九斗二升,问筑堤几日”
只云初日差六十四人,次日转多七人,每人日支米三升,共支米四百三石九斗二升,问筑堤几日”![]() 其大意为:“官府陆续派遣
其大意为:“官府陆续派遣![]() 人前往修筑堤坝,第一天派出
人前往修筑堤坝,第一天派出![]() 人,从第二天开始,每天派出的人数比前一天多
人,从第二天开始,每天派出的人数比前一天多![]() 人,修筑堤坝的每人每天分发大米
人,修筑堤坝的每人每天分发大米![]() 升,共发出大米
升,共发出大米![]() 升,问修筑堤坝多少天”
升,问修筑堤坝多少天”![]() 这个问题中,前
这个问题中,前![]() 天一共应发大米____________升.
天一共应发大米____________升.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com