【题目】某同学用“五点法”画函数f（x）＝Asin（ωx+φ）（ω＞0，|φ|）在某一个周期内的图象时，列表并填入了部分数据，如表：

（1）请将上表数据补充完整，并直接写出函数f（x）的解析式；

（2）将y＝f（x）图象上所有点向左平移θ（θ＞0）个单位长度，得到y＝g（x）的图象.若y＝g（x）图象的一个对称中心为（，0），求θ的最小值.

（3）若，求的值.

【题目】如图，在三棱柱中，平面ABC，，E是BC的中点，．

求异面直线AE与所成的角的大小；

若G为中点，求二面角的余弦值．

【题目】已知函数 ．

（1）当时，函数恒有意义，求实数的取值范围；

（2）是否存在这样的实数，使得函数f（x）在区间上为减函数，并且最大值为？如果存在，试求出的值；如果不存在，请说明理由．

现有李某月收入为18000元，膝下有一名子女在读高三，需赡养老人，除此之外无其它专项附加扣除，则他该月应交纳的个税金额为（ ）

A.1800B.1000C.790D.560

【题目】已知函数的最大值为， 的图像关于轴对称.

（1）求实数， 的值.

（2）设，则是否存在区间，使得函数在区间上的值域为？若存在，求实数的取值范围；若不存在，请说明理由.

【题目】国内某知名大学有男生14000人，女生10000人.该校体育学院想了解本校学生的运动状况，根据性别采取分层抽样的方法从全校学生中抽取120人，统计他们平均每天运动的时间（已知该校学生平均每天运动的时间范围是 ），如下表所示.

男生平均每天运动的时间分布情况：

女生平均每天运动的时间分布情况：

（1）假设同组中的每个数据均可用该组区间的中间值代替，请根据样本估算该校男生平均每天运动的时间（结果精确到0.1）.

（2）若规定平均每天运动的时间不少于的学生为“运动达人”，低于的学生为“非运动达人”.

（ⅰ）根据样本估算该校“运动达人”的数量；

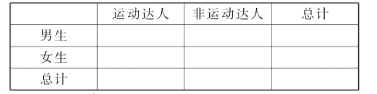
（ⅱ）请根据上述表格中的统计数据填写下面列联表，并通过计算判断能否在犯错误的概率不超过0.05的前提下认为“运动达人”与性别有关.

参考公式： ，其中.

参考数据：

【题目】探究与发现：为什么二次函数的图象是抛物线？我们知道，平面内与一个定点F和一条定直线l距离相等的点的轨迹是抛物线，这是抛物线的定义，也是其本质特征因此，只要说明二次函数的图象符合抛物线的本质特征，就解决了为什么二次函数的图象是抛物线的问题进一步讲，由抛物线与其方程之间的关系可知，如果能用适当的方式将转化为抛物线标准方程的形式，那么就可以判定二次函数的图象是抛物线了．下面我们就按照这个思路来展开．对二次函数式的右边配方，得．由函数图象平移一般地，设是坐标平面内的一个图形，将上所有点按照同一方向，移动同样的长度，得到图形，这一过程叫作图形的平移的知识可以知道，沿向量平移函数的图象如图，函数图象的形状、大小不发生任何变化，平移后图象对应的函数解析式为，我们把它改写为的形式方程，这是顶点为坐标原点，焦点为的抛物线．这样就说明了二次函数的图象是一条抛物线．

请根据以上阅读材料，回答下列问题：

由函数的图象沿向量平移，得到的图象对应的函数解析式为，求的坐标；

过抛物线的焦点F的一条直线交抛物线于P、Q两点若线段PF与QF的长分别是p、q，试探究是否为定值？并说明理由．

【题目】如图，在平行四边形中，，，以为折痕将△折起，使点到达点的位置，且．

（1）证明：平面平面；

（2）为线段上一点，为线段上一点，且，求三棱锥的体积．

【题目】已知数列满足，，设．

（1）求；

（2）判断数列是否为等比数列，并说明理由；

（3）求的通项公式．

已知函数.

（Ⅰ）当时，求的解集；

（Ⅱ）当时， 恒成立，求实数的取值范围.