
科目: 来源: 题型:
【题目】已知下列命题:
①回归直线![]() 恒过样本点的中心
恒过样本点的中心![]() ,且至少过一个样本点;
,且至少过一个样本点;
②两个变量相关性越强,则相关系数![]() 就越接近于
就越接近于![]() ;
;
③对分类变量![]() 与
与![]() ,
,![]() 的观测值
的观测值![]() 越小,“
越小,“![]() 与
与![]() 有关系”的把握程度越大;
有关系”的把握程度越大;
④两个模型中残差平方和越小的模型拟合的效果越好.则正确命题的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】三角形面积为S=![]() (a+b+c)r,a,b,c为三角形三边长,r为三角形内切圆半径,利用类比推理,可以得出四面体的体积为 ( )
(a+b+c)r,a,b,c为三角形三边长,r为三角形内切圆半径,利用类比推理,可以得出四面体的体积为 ( )
A. V=![]() abc B. V=
abc B. V=![]() Sh
Sh
C. V=![]() (ab+bc+ac)·h(h为四面体的高) D. V=
(ab+bc+ac)·h(h为四面体的高) D. V=![]() (S1+S2+S3+S4)·r(其中S1,S2,S3,S4分别为四面体四个面的面积,r为四面体内切球的半径,设四面体的内切球的球心为O,则球心O到四个面的距离都是r)
(S1+S2+S3+S4)·r(其中S1,S2,S3,S4分别为四面体四个面的面积,r为四面体内切球的半径,设四面体的内切球的球心为O,则球心O到四个面的距离都是r)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线![]() ,曲线
,曲线![]() ,且
,且![]() 与
与![]() 的焦点之间的距离为
的焦点之间的距离为![]() ,且
,且![]() 与
与![]() 在第一象限的交点为
在第一象限的交点为![]() .
.
(1)求曲线![]() 的方程和点
的方程和点![]() 的坐标;
的坐标;
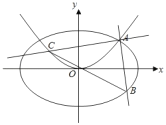
(2)若过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,过点
,过点![]() 与
与![]() 垂直的直线与
垂直的直线与![]() 的另一个交点为
的另一个交点为![]() .设
.设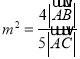 ,试求
,试求![]() 取值范围.
取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】刘徽是我国魏晋时期著名的数学家,他编著的《海岛算经》中有一问题:“今有望海岛,立两表齐,高三丈,前后相去千步,令后表与前表相直。从前表却行一百二十三步,人目著地取望岛峰,与表末参合。从后表却行百二十七步,人目著地取望岛峰,亦与表末参合。问岛高几何?” 意思是:为了测量海岛高度,立了两根表,高均为5步,前后相距1000步,令后表与前表在同一直线上,从前表退行123步,人恰观测到岛峰,从后表退行127步,也恰观测到岛峰,则岛峰的高度为( )(注:3丈=5步,1里=300步)
A. 4里55步 B. 3里125步 C. 7里125步 D. 6里55步
查看答案和解析>>
科目: 来源: 题型:
【题目】某厂每月生产一种投影仪的固定成本为![]() 万元,但每生产
万元,但每生产![]() 台,需要加可变成本(即另增加投入)
台,需要加可变成本(即另增加投入)![]() 万元,市场对此产品的月需求量为
万元,市场对此产品的月需求量为![]() 台,销售的收入函数为
台,销售的收入函数为![]() (万元)
(万元)![]() 且
且![]() ,其中
,其中![]() 是产品售出的数量(单位:百台).
是产品售出的数量(单位:百台).
(1)求月销售利润![]() (万元)关于月产量
(万元)关于月产量![]() (百台)的函数解析式;
(百台)的函数解析式;
(2)当月产量为多少时,销售利润可达到最大?最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com