
科目: 来源: 题型:
【题目】某地区工会利用 “健步行APP”开展健步走积分奖励活动.会员每天走5千步可获积分30分(不足5千步不积分),每多走2千步再积20分(不足2千步不积分).为了解会员的健步走情况,工会在某天从系统中随机抽取了1000名会员,统计了当天他们的步数,并将样本数据分为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 九组,整理得到如下频率分布直方图:
九组,整理得到如下频率分布直方图:
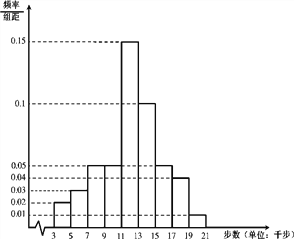
(Ⅰ)求当天这1000名会员中步数少于11千步的人数;
(Ⅱ)从当天步数在![]() ,
, ![]() ,
, ![]() 的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于200分的概率;
的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于200分的概率;
(Ⅲ)写出该组数据的中位数(只写结果).
查看答案和解析>>
科目: 来源: 题型:
【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选出了三个科目作为选考科目.若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:

(Ⅰ)试估计该学校高一年级确定选考生物的学生有多少人?
(Ⅱ)写出选考方案确定的男生中选择“物理、化学和地理”的人数.(直接写出结果)
(Ⅲ)从选考方案确定的男生中任选2名,试求出这2名学生选考科目完全相同的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆C:(x﹣a)2+(y﹣b)2=1(a>0)关于直线3x﹣2y=0对称,且与直线3x﹣4y+1=0相切.
(1)求圆C的方程;
(2)若直线l:y=kx+2与圆C交于M,N两点,是否存在直线l,使得![]() (O为坐标原点)若存在,求出k的值;若不存在,请说明理由.
(O为坐标原点)若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() ,
,![]() ,且
,且![]() .
.
(1)当![]() 时,函数
时,函数![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 平行,试求m的值;
平行,试求m的值;
(2)当![]() 时,令
时,令![]() ,若函数
,若函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,试讨论函数
时,试讨论函数![]() 的零点个数,并证明你的结论.
的零点个数,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为了分析在一次数学竞赛中甲、乙两个班的数学成绩,分别从甲、乙两个班中随机抽取了10个学生的成绩,成绩的茎叶图如下:

(Ⅰ)根据茎叶图,计算甲班被抽取学生成绩的平均值![]() 及方差
及方差![]() ;
;
(Ⅱ)若规定成绩不低于90分的等级为优秀,现从甲、乙两个班级所抽取成绩等级为优秀的学生中,随机抽取2人,求这两个人恰好都来自甲班的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在即将进入休渔期时,某小微企业决定囤积一些冰鲜产品,销售所囤积产品的净利润f(x)万元与投入x万元之间近似满足函数关系: ,若投入2万元,可得到净利润为5.2万元.
,若投入2万元,可得到净利润为5.2万元.
(1)试求该小微企业投入多少万元时,获得的净利润最大;
(2)请判断该小微企业是否会亏本,若亏本,求出投入资金的范围,若不亏本,请说明理由.(参考数据:ln 2≈0.7,ln 15≈2.7)
查看答案和解析>>
科目: 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据
(吨)标准煤的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: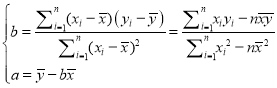
查看答案和解析>>
科目: 来源: 题型:
【题目】某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(I)求直方图中的a值;
(II)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com