
科目: 来源: 题型:
【题目】已知二次函数![]() (
(![]() 、
、![]() 为常数且
为常数且![]() ),满足条件
),满足条件![]() ,且方程
,且方程![]() 有等根.
有等根.
(1)若![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,
,![]() ,使
,使![]() 当定义域为
当定义域为![]() 时,值域为
时,值域为![]() ?如果存在,求出
?如果存在,求出![]() ,
,![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点为极点,以
为参数),以直角坐标系的原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,已知直线
轴的正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)若![]() 与曲线
与曲线![]() 相切,且
相切,且![]() 与坐标轴交于
与坐标轴交于![]() 两点,求以
两点,求以![]() 为直径的圆的极坐标方程.
为直径的圆的极坐标方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】某大型超市在2018年元旦举办了一次抽奖活动,抽奖箱里放有2个红球,1个黄球和1个蓝球(这些小球除颜色外大小形状完全相同),从中随机一次性取2个小球,每位顾客每次抽完奖后将球放回抽奖箱.活动另附说明如下:
①凡购物满100(含100)元者,凭购物打印凭条可获得一次抽奖机会;
②凡购物满188(含188)元者,凭购物打印凭条可获得两次抽奖机会;
③若取得的2个小球都是红球,则该顾客中得一等奖,奖金是一个10元的红包;
④若取得的2个小球都不是红球,则该顾客中得二等奖,奖金是一个5元的红包;
⑤若取得的2个小球只有1个红球,则该顾客中得三等奖,奖金是一个2元的红包.
抽奖活动的组织者记录了该超市前20位顾客的购物消费数据(单位:元),绘制得到如图所示的茎叶图.

(1)求这20位顾客中获得抽奖机会的人数与抽奖总次数(假定每位获得抽奖机会的顾客都会去抽奖);
(2)求这20位顾客中奖得抽奖机会的顾客的购物消费数据的中位数与平均数(结果精确到整数部分);
(3)分别求在一次抽奖中获得红包奖金10元,5元,2元的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某城市理论预测2014年到2018年人口总数![]() (单位:十万)与年份(用
(单位:十万)与年份(用![]() 表示)的关系如表所示:
表示)的关系如表所示:
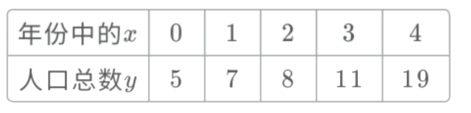
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(3)据此估计2019年该城市人口总数.
(参考数据: ![]()
![]() )
)
参考公式:线性回归方程为![]() ,其中
,其中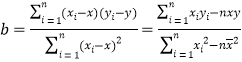 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校![]() 名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是
名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
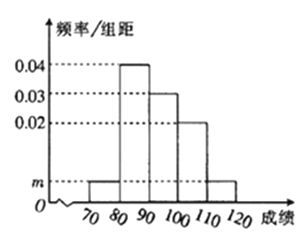
![]() 求图中
求图中![]() 的值;
的值;
![]() 根据频率分布直方图,估计这
根据频率分布直方图,估计这![]() 名学生的平均分;
名学生的平均分;
![]() 若这
若这![]() 名学生的数学成绩中,某些分数段的人数
名学生的数学成绩中,某些分数段的人数![]() 与英语成绩相应分数段的人数
与英语成绩相应分数段的人数![]() 之比如表所示,求英语成绩在
之比如表所示,求英语成绩在![]() 的人数.
的人数.
分数段 |
|
|
|
|
| 1:2 | 1:1 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ( x R ,且 e 为自然对数的底数).
( x R ,且 e 为自然对数的底数).
⑴ 判断函数 f x 的单调性与奇偶性;
⑵是否存在实数 t ,使不等式![]() 对一切的 x R 都成立?若存在,求出 t 的值,若 不存在说明理由.
对一切的 x R 都成立?若存在,求出 t 的值,若 不存在说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数![]() 满足①对于任意
满足①对于任意![]() ,都有
,都有![]() ;②
;②![]() ;③
;③![]() 的图像与
的图像与![]() 轴的两个交点之间的距离为4.
轴的两个交点之间的距离为4.
(1)求![]() 的解析式;
的解析式;
(2)记![]()
①若![]() 为单调函数,求
为单调函数,求![]() 的取值范围;
的取值范围;
②记![]() 的最小值为
的最小值为![]() ,讨论函数
,讨论函数![]() 零点的个数.
零点的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com