(1)求函数g(x)的定义域；

(2)若f(x)是奇函数，且在定义域上单调递减，求不等式g(x)≤0的解集．

【题目】莱市在市内主于道北京路一侧修建圆形休闲广场.如图，圆形广场的圆心为，半径为，并与北京路一边所在直线相切于点.点为上半圆弧上一点，过点作的垂线，垂足为点.市园林局计划在内进行绿化，设的面积为（单位：），（单位：弧度）.

（1）将表示为的函数；

（2）当绿化面积最大时，试确定点的位置，并求最大面积.

（1）当4个舞蹈节目接在一起时，有多少种不同的节目安排顺序？

（2）当要求每2个舞蹈节目之间至少安排1个演唱节目时，有多少种不同的节目安排顺序？

（3）若已定好节目单，后来情况有变，需加上诗歌朗诵和快板2个节目，但不能改变原来节目的相对顺序，有多少种不同的节目演出顺序？

（1）分别求甲乙两个小组成绩的平均数与方差；

（2）分析比较甲乙两个小组的成绩；

（3）从甲组高于70分的同学中，任意抽取2名同学，求恰好有一名同学的得分在[80,90）的概率．

如果统计资料表明y与x有线性相关关系，试求：

（Ⅰ）求相关系数（精确到0.01）；

（Ⅱ）求线性回归方程（精确到0.01）；

（III）若发生火灾的某居民区与最近的消防站相距10.0千米，评估一下火灾的损失（精确到0.01）.

参考数据：，，，

，，

参考公式：相关系数 ，回归方程 中斜率和截距的最小二乘估计公式分别为：，

【题目】已知点，圆：，点是圆上一动点，线段的垂直平分线与交于点.

（1）求点的轨迹的方程；

（2）曲线与轴交于点，，直线过点且垂直于轴，点在直线上，点在曲线上，若，试判断直线与曲线的交点的个数.

【题目】设函数.

（1）求函数的单调区间；

（2）若存在、满足.求证： （其中为的导函数）

【题目】某种产品，每售出一吨可获利万元，每积压一吨则亏损万元.某经销商统计出过去年里市场年需求量的频数分布表如下表所示.

（1）求过去年年需求量的平均值；（每个区间的年需求量用中间值代替）

（2）今年该经销商欲进货吨，以（单位：吨，）表示今年的年需求量，以（单位：万元）表示今年销售的利润，试将表示的函数解析式，并求今年的年利润不少于万元的概率.

【题目】已知圆，直线过点

（1）若直线的斜率为，证明：与圆相切；

（2）若直线与圆交于两点，且，求直线的斜率．

【题目】如图，已知椭圆： 的离心率为，上、下顶点分别为、，点在椭圆上，且异于点、，直线、与直线： 分别交于点、，且面积的最大值为.

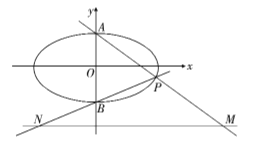
（1）求椭圆的标准方程；

（2）求线段的长的最小值.