
科目: 来源: 题型:
【题目】小明口袋中有3张10元,3张20元(因纸币有编号认定每张纸币不同),现从中掏出纸币超过45元的方法有_______种;若小明每次掏出纸币的概率是等可能的,不放回地掏出4张,刚好是50元的概率为_______.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数![]() (
(![]() ,且
,且![]() )是定义域为R的奇函数.
)是定义域为R的奇函数.
(1)求t的值;
(2)若![]() ,求使不等式
,求使不等式![]() 对一切
对一切![]() 恒成立的实数k的取值范围;
恒成立的实数k的取值范围;
(3)若函数![]() 的图象过点
的图象过点![]() ,是否存在正数m(
,是否存在正数m(![]() ),使函数
),使函数![]() 在
在![]() 上的最大值为0,若存在,求出m的值;若不存在,请说明理由.
上的最大值为0,若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年1月8日,中共中央国务院隆重举行国家科学技术奖励大会,在科技界引发热烈反响,自主创新正成为引领经济社会发展的强劲动力.某科研单位在研发新产品的过程中发现了一种新材料,由大数据测得该产品的性能指标值y与这种新材料的含量x(单位:克)的关系为:当![]() 时,y是x的二次函数;当
时,y是x的二次函数;当![]() 时,
时,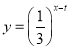 测得数据如下表(部分):
测得数据如下表(部分):
x(单位:克) | 0 | 1 | 2 | 9 | … |
y | 0 |
| 3 |
| … |
(1)求y关于x的函数关系式![]() ;
;
(2)当该产品中的新材料含量x为何值时,产品的性能指标值最大.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地下车库在排气扇发生故障的情况下,测得空气中一氧化碳含量达到了危险状态,经抢修,排气扇恢复正常.排气![]() 后,测得车库内的一氧化碳浓度为
后,测得车库内的一氧化碳浓度为![]() ,继续排气
,继续排气![]() ,又测得浓度为
,又测得浓度为![]() ,经检测知该地下车库一氧化碳浓度
,经检测知该地下车库一氧化碳浓度![]() 与排气时间
与排气时间![]() 存在函数关系:
存在函数关系: (
(![]() ,
,![]() 为常数)。
为常数)。
(1)求![]() ,
,![]() 的值;
的值;
(2)若地下车库中一氧化碳浓度不高于![]() 为正常,问至少排气多少分钟,这个地下车库中的一氧化碳含量才能达到正常状态?
为正常,问至少排气多少分钟,这个地下车库中的一氧化碳含量才能达到正常状态?
查看答案和解析>>
科目: 来源: 题型:
【题目】科技改变生活,方便生活.共享单车的使用就是云服务的一种实践,它是指企业与政府合作,为居民出行提供单车共享服务,它符合低碳出行理念,为解决城市出行的“最后一公里”提供了有力支撑,是共享经济的一种新形态.某校学生社团为研究当地使用共享单车人群的年龄状况,随机抽取了当地![]() 名使用共享单车的群众作出调查,所得频率分布直方图如图所示.
名使用共享单车的群众作出调查,所得频率分布直方图如图所示.
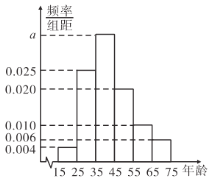
(1)估计当地共享单车使用者年龄的中位数;
(2)若按照分层抽样从年龄在![]() ,
,![]() 的人群中抽取
的人群中抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人调查单车使用体验情况,记抽取的
人调查单车使用体验情况,记抽取的![]() 人中年龄在
人中年龄在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线
的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线![]() :
: ![]() 与椭圆
与椭圆![]() 有且只有一个公共点.
有且只有一个公共点.
(Ⅰ)求椭圆![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(Ⅱ)设![]() 是坐标原点,直线
是坐标原点,直线![]() 平行于
平行于![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且与直线
,且与直线![]() 交于点
交于点![]() ,证明:存在常数
,证明:存在常数![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某媒体为调查喜爱娱乐节目A是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
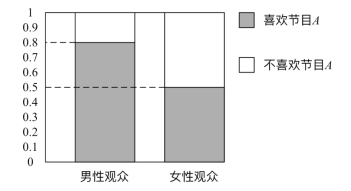
根据该等高条形图,完成下列2×2列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目A与观众性别有关?
喜欢节目A | 不喜欢节目A | 总计 | |
男性观众 | |||
女性观众 | |||
总计 | 60 |
附: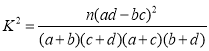
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】设有三个乡镇,分别位于一个矩形![]() 的两个顶点M,N及
的两个顶点M,N及![]() 的中点S处,
的中点S处,![]() ,现要在该矩形的区域内(含边界),且与M,N等距离的一点O处设一个宣讲站,记O点到三个乡镇的距离之和为
,现要在该矩形的区域内(含边界),且与M,N等距离的一点O处设一个宣讲站,记O点到三个乡镇的距离之和为![]() .
.
(1)设![]() ,试将L表示为x的函数并写出其定义域;
,试将L表示为x的函数并写出其定义域;
(2)试利用(1)的函数关系式确定宣讲站O的位置,使宣讲站O到三个乡镇的距离之和![]() 最小.
最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com