
科目: 来源: 题型:
【题目】下表为![]() 年至
年至![]() 年某百货零售企业的线下销售额(单位:万元),其中年份代码
年某百货零售企业的线下销售额(单位:万元),其中年份代码![]() 年份
年份![]() .
.
年份代码 |
|
|
|
|
线下销售额 |
|
|
|
|
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 年该百货零售企业的线下销售额;
年该百货零售企业的线下销售额;
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了![]() 位男顾客、
位男顾客、![]() 位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有
位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有![]() 人、女顾客有
人、女顾客有![]() 人,能否在犯错误的概率不超过
人,能否在犯错误的概率不超过![]() 的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
参考公式及数据: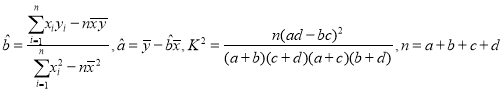 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法中正确的是( )
A.对具有线性相关关系的变量![]() 有一组观测数据
有一组观测数据![]() ,其线性回归方程是
,其线性回归方程是![]() ,且
,且![]() ,则实数
,则实数![]() 的值是
的值是![]()
B.正态分布![]() 在区间
在区间![]() 和
和![]() 上取值的概率相等
上取值的概率相等
C.若两个随机变量的线性相关性越强,则相关系数![]() 的值越接近于1
的值越接近于1
D.若一组数据![]() 的平均数是2,则这组数据的众数和中位数都是2
的平均数是2,则这组数据的众数和中位数都是2
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为![]() 的样本,得到一周参加社区服务的时间的统计数据好下表:
的样本,得到一周参加社区服务的时间的统计数据好下表:
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
(Ⅰ)求![]() ,
,![]() ;
;
(Ⅱ)能否有95%的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
(Ⅲ)以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率,现从该校学生中随机调查6名学生,试估计6名学生中一周参加社区服务时间超过1小时的人数.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直角坐标系![]() 的原点和极坐标系
的原点和极坐标系![]() 的极点重合,
的极点重合,![]() 轴非负半轴与极轴重合, 单位长度相同, 在直角坐标系下, 曲线
轴非负半轴与极轴重合, 单位长度相同, 在直角坐标系下, 曲线![]() 的参数方程为
的参数方程为![]() ,
,![]() 为参数) .
为参数) .
(1) 写出曲线![]() 的极坐标方程;
的极坐标方程;
(2) 直线![]() 的极坐标方程为
的极坐标方程为![]() ,求曲线
,求曲线![]() 与直线
与直线![]() 在平面直角坐标系中的交点坐标 .
在平面直角坐标系中的交点坐标 .
查看答案和解析>>
科目: 来源: 题型:
【题目】一个大于1的自然数,除了1和它本身外,不能被其他自然数整除,则称这个数为质数.质数的个数是无穷的.设由所有质数组成的无穷递增数列![]() 的前
的前![]() 项和为
项和为![]() ,等差数列1,3,5,7,…中所有不大于
,等差数列1,3,5,7,…中所有不大于![]() 的项的和为
的项的和为![]() .
.
(Ⅰ)求![]() 和
和![]() ;
;
(Ⅱ)判断![]() 和
和![]() 的大小,不用证明;
的大小,不用证明;
(Ⅲ)设![]() ,求证:
,求证:![]() ,
,![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过
,过![]() 且与
且与![]() 轴垂直的直线被椭圆
轴垂直的直线被椭圆![]() 和圆
和圆![]() 截得的弦长分别为2和
截得的弦长分别为2和![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)已知动直线![]() 与抛物线
与抛物线![]() :
:![]() 相切(切点异于原点),且
相切(切点异于原点),且![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,问:椭圆
两点,问:椭圆![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在求出满足条件的所有
,若存在求出满足条件的所有![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com