(1)分别计算按这两种方案所建的仓库的体积；

(2)分别计算按这两种方案所建的仓库的表面积；

(3)哪个方案更经济些？

【题目】美国制裁中兴，未来7年一颗芯片都不卖，这却激发了中国“芯”的研究热潮.某公司甲，乙，丙三个研发小组分别研发，，三种不同的芯片，现在用分层抽样的方法从这些芯片中抽取若干件进行质量分析，有关数据见下表（单位：件）.

（Ⅰ）求的值；

（Ⅱ）若在这抽出的样品中随机抽取2件送往某机构进行进一步检测，求这2件芯片来自不同种类的概率.

【题目】如图所示，多面体ABCDEF中，已知平面ABCD是边长为3的正方形，，，EF到平面ABCD的距离为2，则该多面体的体积V为（ ）

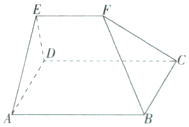
A.B.5C.6D.

【题目】如图所示，在直三棱柱中，，，，为线段的中点.

（Ⅰ）证明：平面；

（Ⅱ）求二面角的正弦值.

【题目】如图，四边形为矩形，平面，，，，.

（Ⅰ）求证：平面；

（Ⅱ）点在线段上，且，过、、三点的平面将多面体分成两部分，设上、下两部分的体积分别为、，求.

【题目】已知函数.

(1)若在上单调递减，求的取值范围；

(2)若在处取得极值，判断当时，存在几条切线与直线平行，请说明理由；

(3)若有两个极值点，求证：.

【题目】已知椭圆的离心率为，椭圆的左焦点为，椭圆上任意点到的最远距离是，过直线与轴的交点任作一条斜率不为零的直线与椭圆交于不同的两点、，点关于轴的对称点为.

(1)求椭圆的方程；

(2)求证：、、三点共线；

(3)求面积的最大值.

【题目】从下面①②③三个条件中任选两个，根据你选择的条件确定一条直线，判断直线与圆的位置关系.

①过点；②斜率为；③在轴和轴上的截距相等.

【题目】在多面体中，四边形是正方形，平面平面，.

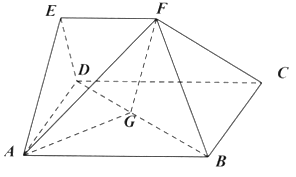
（1）求证：平面；

（2）在线段上是否存在点，使得平面与平面所成的锐二面角的大小为，若存在，求出的值；若不存在，说明理由.

【题目】如图所示，在四棱锥中，是边长为的正三角形，点为正方形的中心，为线段的中点，.则下列结论正确的是（ ）

A.平面平面

B.直线与是异面直线

C.线段与的长度相等

D.直线与平面所成的角的余弦值为