【题目】已知抛物线的焦点到准线的距离为，直线与抛物线交于，两点，过这两点分别作抛物线的切线，且这两条切线相交于点．

（1）若点的坐标为，求的值；

（2）设线段的中点为，过的直线与线段为直径的圆相切，切点为，且直线与抛物线交于，两点，求的取值范围．

【题目】如图①，在等腰梯形中，，，分别为，的中点，，为中点现将四边形沿折起,使平面平面，得到如图②所示的多面体在图②中，

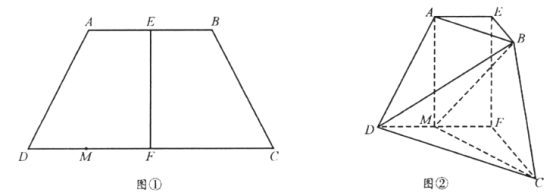
（1）证明：；

（2）求二面角的余弦值。

(1)求函数的单调区间；

(2)设h(x)＝f′(x)＋，若h(x)>k(k∈Z)恒成立，求k的最大值．

（1）在这5年中随机抽取两年，求平均每台设备每年的维护费用至少有1年多于2万元的概率；

（2）求关于的线性回归方程．若该设备的价格是每台16万元，你认为应该使用满五年换一次设备，还是应该使用满八年换一次设备？请说明理由．

参考公式：用最小二乘法求线性回归方程的系数公式．

【题目】在直角坐标系中，直线的参数方程为（为参数），以原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

（1）分别写出直线的普通方程与曲线的直角坐标方程；

（2）已知点，直线与曲线相交于两点，求证：.

（1）记汽车选择公路1运送啤酒时厂家获得的毛收入为X（单位：万元），求X的分布列和EX；

（2）若，，选择哪条公路运送啤酒厂家获得的毛收人更多？

（注：毛收入=销售商支付给厂家的费用-运费）．

【题目】设各项均为正数的数列{an}的前n项和为Sn，满足：对任意的n∈N*，都有an+1+Sn+1＝1，又a1．

（1）求数列{an}的通项公式；

（2）令bn＝log2an，求（n∈N*）

【题目】已知抛物线的焦点到准线的距离为，直线与抛物线交于，两点，过这两点分别作抛物线的切线，且这两条切线相交于点．

（1）若点的坐标为，求的值；

（2）设线段的中点为，过的直线与线段为直径的圆相切，切点为，且直线与抛物线交于，两点，求的取值范围．

（1）在这5年中随机抽取两年，求平均每台设备每年的维护费用至少有1年多于2万元的概率；

（2）求关于的线性回归方程．若该设备的价格是每台16万元，你认为应该使用满五年换一次设备，还是应该使用满八年换一次设备？请说明理由．

参考公式：用最小二乘法求线性回归方程的系数公式．

【题目】已知函数.

（1）证明：函数在上存在唯一的零点；

（2）若函数在区间上的最小值为1，求的值.