
科目: 来源: 题型:
【题目】已知数列![]() 是由正整数组成的无穷数列.若存在常数
是由正整数组成的无穷数列.若存在常数![]() ,使得
,使得![]() 任意的
任意的![]() 成立,则称数列
成立,则称数列![]() 具有性质
具有性质![]() .
.
(1)分别判断下列数列![]() 是否具有性质
是否具有性质![]() ; (直接写出结论)
; (直接写出结论)
①![]()
②![]()
(2)若数列![]() 满足
满足![]() ,求证:“数列
,求证:“数列![]() 具有性质
具有性质![]() ”是“数列
”是“数列![]() 为常数列”的充分必要条件;
为常数列”的充分必要条件;
(3)已知数列![]() 中
中![]() 且
且![]() .若数列
.若数列![]() 具有性质
具有性质![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,
,![]() 的面积为2.
的面积为2.
(I)求椭圆C的方程;
(II)设M是椭圆C上一点,且不与顶点重合,若直线![]() 与直线
与直线![]() 交于点P,直线
交于点P,直线![]() 与直线
与直线![]() 交于点Q.求证:△BPQ为等腰三角形.
交于点Q.求证:△BPQ为等腰三角形.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(I)当a=-1时,
①求曲线y= f(x)在点(0,f(0))处的切线方程;
②求函数f(x)的最小值;
(II)求证:当![]() 时,曲线
时,曲线![]() 与
与![]() 有且只有一个交点.
有且只有一个交点.
查看答案和解析>>
科目: 来源: 题型:
【题目】科技创新能力是决定综合国力和国际竞争力的关键因素,也是推动经济实现高质量发展的重要支撑,而研发投入是科技创新的基本保障,下图是某公司从2010年到2019年这10年研发投入的数据分布图:

其中折线图是该公司研发投入占当年总营收的百分比,条形图是当年研发投入的数值(单位:十亿元).
(I)从2010年至2019年中随机选取一年,求该年研发投入占当年总营收的百分比超过10%的概率;
(II)从2010年至2019年中随机选取两个年份,设X表示其中研发投入超过500亿元的年份的个数,求X的分布列和数学期望;
(III)根据图中的信息,结合统计学知识,判断该公司在发展的过程中是否比较重视研发,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知a,b,c为正数,f(x)=|x+a|+|x+b|+|x﹣c|.
(1)若a=b=c=1,求函数f(x)的最小值;
(2)若f(0)=1且a,b,c不全相等,求证:b3c+c3a+a3b>abc.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=axlnx﹣x2﹣ax+1(a∈R)在定义域内有两个不同的极值点.
(1)求实数a的取值范围;
(2)设两个极值点分别为x1,x2,x1<x2,证明:f(x1)+f(x2)<2﹣x12+x22.
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年春,新型冠状病毒在我国湖北武汉爆发并讯速蔓延,病毒传染性强并严重危害人民生命安全,国家卫健委果断要求全体人民自我居家隔离,为支援湖北武汉新型冠状病毒疫情防控工作,各地医护人员纷纷逆行,才使得病毒蔓延得到了有效控制.某社区为保障居民的生活不受影响,由社区志愿者为其配送蔬菜、大米等生活用品,记者随机抽查了男、女居民各100名对志愿者所买生活用品满意度的评价,得到下面的2×2列联表.
特别满意 | 基本满意 | |
男 | 80 | 20 |
女 | 95 | 5 |
(1)被调查的男性居民中有5个年轻人,其中有2名对志愿者所买生活用品特别满意,现在这5名年轻人中随机抽取3人,求至多有1人特别满意的概率.
(2)能否有99%的把握认为男、女居民对志愿者所买生活用品的评价有差异?
附: 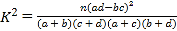
|
|
|
|
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,M,M1分别为AB,A1B1中点.
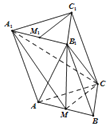
(1)求证:C1M1∥面A1MC;
(2)若面ABC⊥面ABB1A1,△AB1B为正三角形,AB=2,BC=1,![]() ,求四棱锥B1﹣AA1C1C的体积.
,求四棱锥B1﹣AA1C1C的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度,某地区在2015年以前的年均脱贫率(脱贫的户数占当年贫困户总数的比)为70%,2015年开始全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加户数占2019年贫困总户数的比)及该项目的脱贫率见下表:
实施项目 | 种植业 | 养殖业 | 工厂就业 |
参加占户比 | 45% | 45% | 10% |
脱贫率 | 96% | 96% | 90% |
那么2019年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )倍.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】四棱锥S-ABCD中,底面ABCD是边长为2的菱形,![]() ,
,![]() ,二面角S-BD-C的余弦值为
,二面角S-BD-C的余弦值为![]() .
.
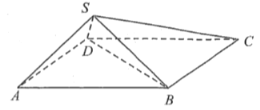
(I)证明:平面![]() 平面SBD;
平面SBD;
(Ⅱ)求二面角A-SD-C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com