
科目: 来源: 题型:
【题目】如果存在常数a,使得数列{an}满足:若x是数列{an}中的一项,则a-x也是数列{an}中的一项,称数列{an}为“兑换数列”,常数a是它的“兑换系数”.
(1)若数列:2,3,6,m(m>6)是“兑换系数”为a的“兑换数列”,求m和a的值;
(2)已知有穷等差数列{bn}的项数是n0(n0≥3),所有项之和是B,求证:数列{bn}是“兑换数列”,并用n0和B表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列{cn},是否有可能它既是等比数列,又是“兑换数列”?给出你的结论,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点F1、F2为双曲线![]() (b>0)的左、右焦点,过F2作垂直于x轴的直线,在x轴上方交双曲线C于点M,且∠MF1F2=30°,圆O的方程是x2+y2=b2.
(b>0)的左、右焦点,过F2作垂直于x轴的直线,在x轴上方交双曲线C于点M,且∠MF1F2=30°,圆O的方程是x2+y2=b2.
(1)求双曲线C的方程;
(2)过双曲线C上任意一点P作该双曲线两条渐近线的垂线,垂足分别为P1、P2,求![]() 的值;
的值;
(3)过圆O上任意一点Q作圆O的切线l交双曲线C于A、B两点,AB中点为M,求证:|AB|=2|OM|.
查看答案和解析>>
科目: 来源: 题型:
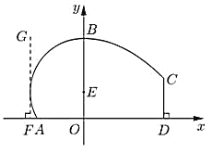
【题目】某地拟建造一座体育馆,其设计方案侧面的外轮廓线如图所示:曲线![]() 是以点
是以点![]() 为圆心的圆的一部分,其中
为圆心的圆的一部分,其中![]()
![]() ,
,![]() 是圆的切线,且
是圆的切线,且![]() ,曲线
,曲线![]() 是抛物线
是抛物线![]()
![]() 的一部分,
的一部分,![]() ,且
,且![]() 恰好等于圆
恰好等于圆![]() 的半径.
的半径.
(1)若![]() 米,
米,![]() 米,求
米,求![]() 与
与![]() 的值;
的值;
(2)若体育馆侧面的最大宽度![]() 不超过75米,求
不超过75米,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
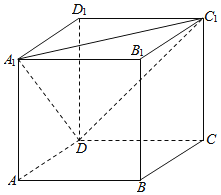
【题目】如图为正方体ABCD-A1B1C1D1,动点M从B1点出发,在正方体表面沿逆时针方向运动一周后,再回到B1的运动过程中,点M与平面A1DC1的距离保持不变,运动的路程x与l=MA1+MC1+MD之间满足函数关系l=f(x),则此函数图象大致是( )
A. 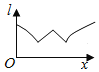 B.
B. 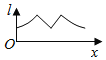
C. 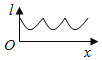 D.
D. 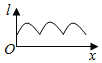
查看答案和解析>>
科目: 来源: 题型:
【题目】设数列![]() 和
和![]() 的项数均为
的项数均为![]() ,则将两个数列的偏差距离定义为
,则将两个数列的偏差距离定义为![]() ,其中
,其中![]() .
.
(1)求数列1,2,7,8和数列2,3,5,6的偏差距离;
(2)设![]() 为满足递推关系
为满足递推关系![]() 的所有数列
的所有数列![]() 的集合,
的集合,![]() 和
和![]() 为
为![]() 中的两个元素,且项数均为
中的两个元素,且项数均为![]() ,若
,若![]() ,
,![]() ,
,![]() 和
和![]() 的偏差距离小于2020,求
的偏差距离小于2020,求![]() 最大值;
最大值;
(3)记![]() 是所有7项数列
是所有7项数列![]() 或
或![]() 的集合,
的集合,![]() ,且
,且![]() 中任何两个元素的偏差距离大于或等于3,证明:
中任何两个元素的偏差距离大于或等于3,证明:![]() 中的元素个数小于或等于16.
中的元素个数小于或等于16.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知椭圆![]() :
:![]() ,左顶点为
,左顶点为![]() ,经过点
,经过点![]() ,过点
,过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
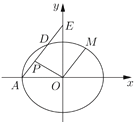
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为
为![]() 的中点,
的中点,![]() ,证明:对于任意的
,证明:对于任意的![]() 都有
都有![]() 恒成立;
恒成立;
(3)若过点![]() 作直线
作直线![]() 的平行线交椭圆
的平行线交椭圆![]() 于点
于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司为了应对金融危机,决定适当进行裁员,已知这家公司现有职工![]() 人(
人(![]() ,且
,且![]() 为10的整数倍),每人每年可创利100千元,据测算,在经营条件不变的前的提下,若裁员人数不超过现有人数的30%,则每裁员1人,留岗员工每人每年就能多创利1千元(即若裁员
为10的整数倍),每人每年可创利100千元,据测算,在经营条件不变的前的提下,若裁员人数不超过现有人数的30%,则每裁员1人,留岗员工每人每年就能多创利1千元(即若裁员![]() 人,留岗员工可多创利润
人,留岗员工可多创利润![]() 千元);若裁员人数超过现有人数的30%,则每裁员1人,留岗员工每人每年就能多创利2千元(即若裁员
千元);若裁员人数超过现有人数的30%,则每裁员1人,留岗员工每人每年就能多创利2千元(即若裁员![]() 人,留岗员工可多创利润
人,留岗员工可多创利润![]() 千元),为保证公司的正常运转,留岗的员工数不得少于现有员工人数的50%,为了保障被裁员工的生活,公司要付给被裁员工每人每年20千元的生活费.
千元),为保证公司的正常运转,留岗的员工数不得少于现有员工人数的50%,为了保障被裁员工的生活,公司要付给被裁员工每人每年20千元的生活费.
(1)设公司裁员人数为![]() ,写出公司获得的经济效益
,写出公司获得的经济效益![]() (千元)关于
(千元)关于![]() 的函数(经济效益=在职人员创利总额—被裁员工生活费);
的函数(经济效益=在职人员创利总额—被裁员工生活费);
(2)为了获得最大的经济效益,该公司应裁员多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:若数列![]() 满足,存在实数
满足,存在实数![]() ,对任意
,对任意![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 有上界,
有上界,![]() 是数列
是数列![]() 的一个上界,已知定理:单调递增有上界的数列收敛(即极限存在).
的一个上界,已知定理:单调递增有上界的数列收敛(即极限存在).
(1)数列![]() 是否存在上界?若存在,试求其所有上界中的最小值;若不存在,请说明理由;
是否存在上界?若存在,试求其所有上界中的最小值;若不存在,请说明理由;
(2)若非负数列![]() 满足
满足![]() ,
,![]() (
(![]() ),求证:1是非负数列
),求证:1是非负数列![]() 的一个上界,且数列
的一个上界,且数列![]() 的极限存在,并求其极限;
的极限存在,并求其极限;
(3)若正项递增数列![]() 无上界,证明:存在
无上界,证明:存在![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人玩猜数字游戏,先由甲心中任想一个数字,记为![]() ,再由乙猜甲刚才想的数字把乙猜的数字记为
,再由乙猜甲刚才想的数字把乙猜的数字记为![]() ,且
,且![]() ,若
,若![]() ,则称甲乙“心有灵犀”,现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________
,则称甲乙“心有灵犀”,现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com