
科目: 来源: 题型:
【题目】设函数![]() 、
、![]() 的定义域均为
的定义域均为![]() ,若对任意
,若对任意![]() ,且
,且![]() ,具有
,具有![]() ,则称函数
,则称函数![]() 为
为![]() 上的单调非减函数,给出以下命题:① 若
上的单调非减函数,给出以下命题:① 若![]() 关于点
关于点![]() 和直线
和直线![]() (
(![]() )对称,则
)对称,则![]() 为周期函数,且
为周期函数,且![]() 是
是![]() 的一个周期;② 若
的一个周期;② 若![]() 是周期函数,且关于直线
是周期函数,且关于直线![]() 对称,则
对称,则![]() 必关于无穷多条直线对称;③ 若
必关于无穷多条直线对称;③ 若![]() 是单调非减函数,且关于无穷多个点中心对称,则
是单调非减函数,且关于无穷多个点中心对称,则![]() 的图象是一条直线;④ 若
的图象是一条直线;④ 若![]() 是单调非减函数,且关于无穷多条平行于
是单调非减函数,且关于无穷多条平行于![]() 轴的直线对称,则
轴的直线对称,则![]() 是常值函数;以上命题中,所有真命题的序号是_________
是常值函数;以上命题中,所有真命题的序号是_________
查看答案和解析>>
科目: 来源: 题型:
【题目】设![]() 是定义在
是定义在![]() 上的函数,若存在
上的函数,若存在![]() ,使得
,使得![]() 在
在![]() 单调递增,在
单调递增,在![]() 上单调递减,则称
上单调递减,则称![]() 为
为![]() 上的单峰函数,
上的单峰函数,![]() 为峰点,包含峰点的区间称为含峰区间,其含峰区间的长度为:
为峰点,包含峰点的区间称为含峰区间,其含峰区间的长度为:![]() .
.
(1)判断下列函数中,哪些是“![]() 上的单峰函数”?若是,指出峰点;若不是,说出原因;
上的单峰函数”?若是,指出峰点;若不是,说出原因;![]() ;
;
(2)若函数![]() 是
是![]() 上的单峰函数,求实数
上的单峰函数,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 是区间
是区间![]() 上的单峰函数,证明:对于任意的
上的单峰函数,证明:对于任意的![]() ,若
,若![]() ,则
,则![]() 为含峰区间;若
为含峰区间;若![]() ,则
,则![]() 为含峰区间;试问当
为含峰区间;试问当![]() 满足何种条件时,所确定的含峰区间的长度不大于0.6.
满足何种条件时,所确定的含峰区间的长度不大于0.6.
查看答案和解析>>
科目: 来源: 题型:
【题目】某小区有一块三角形空地,如图△ABC,其中AC=180米,BC=90米,∠C=90°,开发商计划在这片空地上进行绿化和修建运动场所,在△ABC内的P点处有一服务站(其大小可忽略不计),开发商打算在AC边上选一点D,然后过点P和点D画一分界线与边AB相交于点E,在△ADE区域内绿化,在四边形BCDE区域内修建运动场所. 现已知点P处的服务站与AC距离为10米,与BC距离为100米. 设![]() 米,试问
米,试问![]() 取何值时,运动场所面积最大?
取何值时,运动场所面积最大?

查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 为坐标原点,圆
为坐标原点,圆![]() ,定点
,定点![]() ,点
,点![]() 是圆
是圆![]() 上一动点,线段
上一动点,线段![]() 的垂直平分线交圆
的垂直平分线交圆![]() 的半径
的半径![]() 于点
于点![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知点![]() 是曲线
是曲线![]() 上但不在坐标轴上的任意一点,曲线
上但不在坐标轴上的任意一点,曲线![]() 与
与![]() 轴的焦点分别为
轴的焦点分别为![]() ,直线
,直线![]() 和
和![]() 分别与
分别与![]() 轴相交于
轴相交于![]() 两点,请问线段长之积
两点,请问线段长之积![]() 是否为定值?如果还请求出定值,如果不是请说明理由;
是否为定值?如果还请求出定值,如果不是请说明理由;
(3)在(2)的条件下,若点![]() 坐标为(-1,0),设过点
坐标为(-1,0),设过点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某烘焙店加工一个成本为60元的蛋糕,然后以每个120元的价格出售,如果当天卖不完,剩下的这种蛋糕作餐厨垃圾处理.
(1)若烘焙店一天加工16个这种蛋糕,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:个,
(单位:个,![]() )的函数解析式;
)的函数解析式;
(2)为了解该种蛋糕的市场需求情况与性別是否有关,随机统计了100人的购买情况,得如下列联表:
男 | 女 | 合计 | |
购买 | 15 | 35 | 50 |
不购买 | 6 | 44 | 50 |
合计 | 21 | 79 | 100 |
问:能否有![]() 的把握认为是否购买蛋糕与性別有关?
的把握认为是否购买蛋糕与性別有关?
附: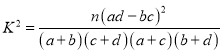
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目: 来源: 题型:
【题目】以平面直角坐标系中的坐标原点为极点,![]() 轴的正半抽为极轴,建立极坐标系,曲线
轴的正半抽为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,直线
,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角
的倾斜角![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com