
科目: 来源: 题型:
【题目】为提高城市居民生活幸福感,某城市公交公司大力确保公交车的准点率,减少居民乘车候车时间为此,该公司对某站台乘客的候车时间进行统计乘客候车时间受公交车准点率、交通拥堵情况、节假日人流量增大等情况影响在公交车准点率正常、交通拥堵情况正常、非节假日的情况下,乘客候车时间随机变量![]() 满足正态分布
满足正态分布![]() 在公交车准点率正常、交通拥堵情况正常、非节假日的情况下,调查了大量乘客的候车时间,经过统计得到如图频率分布直方图.
在公交车准点率正常、交通拥堵情况正常、非节假日的情况下,调查了大量乘客的候车时间,经过统计得到如图频率分布直方图.
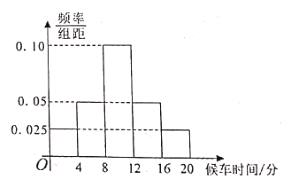
(1)在直方图各组中,以该组区间的中点值代表该组中的各个值,试估计![]() 的值;
的值;
(2)在统计学中,发生概率低于千分之三的事件叫小概率事件,一般认为,在正常情况下,一次试验中,小概率事件是不能发生的在交通拥堵情况正常、非节假日的某天,随机调查了该站的10名乘客的候车时间,发现其中有3名乘客候车时间超过15分钟,试判断该天公交车准点率是否正常,说明理由.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】近一段时间来,由于受非洲猪瘟的影响,各地猪肉价格普遍上涨,生猪供不应求。各大养猪场正面临巨大挑战,目前各项针对性政策措施对于生猪整体产能恢复、激发养殖户积极性的作用正在逐步显现.
现有甲、乙两个规模一致的大型养猪场,均养有1万头猪.根据猪的重量,将其分为三个成长阶段如下表.
猪生长的三个阶段
阶段 | 幼年期 | 成长期 | 成年期 |
重量(Kg) |
|
|
|
根据以往经验,两个养猪场内猪的体重![]() 均近似服从正态分布
均近似服从正态分布![]()
![]() .
.
由于我国有关部门加强对大型养猪场即将投放市场的成年期的猪监控力度,高度重视其质量保证,为了养出健康的成年活猪,甲、乙两养猪场引入两种不同的防控及养殖模式.已知甲、乙两个养猪场内一头成年期猪能通过质检合格的概率分别为![]() ,
,![]() .
.
(1)试估算各养猪场三个阶段的猪的数量;
(2)已知甲养猪场出售一头成年期的猪,若为健康合格的猪 ,则可盈利![]() 元,若为不合格的猪,则亏损
元,若为不合格的猪,则亏损![]() 元;乙养猪场出售一头成年期的猪,若为健康合格的猪 ,则可盈利
元;乙养猪场出售一头成年期的猪,若为健康合格的猪 ,则可盈利![]() 元,若为不合格的猪,则亏损
元,若为不合格的猪,则亏损![]() 元.记
元.记![]() 为甲、乙养猪场各出售一头成年期猪所得的总利润,求随机变量
为甲、乙养猪场各出售一头成年期猪所得的总利润,求随机变量![]() 的分布列,假设两养猪场均能把成年期猪售完,求两养猪场的总利润期望值.
的分布列,假设两养猪场均能把成年期猪售完,求两养猪场的总利润期望值.
(参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】下列有关命题的说法正确的是( )
A.若“![]() ”为假命题,则“
”为假命题,则“![]() ”为假命题
”为假命题
B.“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
C.命题“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
D.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左焦点
的左焦点![]() ,离心率为
,离心率为![]() ,点P为椭圆E上任一点,且
,点P为椭圆E上任一点,且![]() 的最大值为
的最大值为![]() .
.
(1)求椭圆E的方程;
(2)若直线l过椭圆的左焦点![]() ,与椭圆交于A,B两点,且
,与椭圆交于A,B两点,且![]() 的面积为
的面积为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,分别记录了3月1日到3月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数y(颗) | 23 | 25 | 30 | 26 | 16 |
他们所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对选取的2组数据进行检验.
(1)求选取的2组数据恰好是相邻2天数据的概率;
(2)若选取的是3月1日与3月5日的两组数据,请根据3月2日至3月4日的数据,求出y关于x的线性回归方程;并预报当温差为![]() 时的种子发芽数.
时的种子发芽数.
参考公式:![]() ,其中
,其中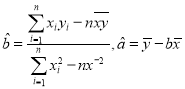
查看答案和解析>>
科目: 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的方程为
的方程为![]() .
.
(1)以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,求曲线
轴的正半轴为极轴建立极坐标系,求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的极坐标方程;
的极坐标方程;
(2)在(1)的条件下,直线![]() 的极坐标方程为
的极坐标方程为![]() ,设曲线
,设曲线![]() 与直线
与直线![]() 的交于点
的交于点![]() 和点
和点![]() ,曲线
,曲线![]() 与直线
与直线![]() 的交于点
的交于点![]() 和点
和点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂每日生产某种产品![]() 吨,当日生产的产品当日销售完毕,当
吨,当日生产的产品当日销售完毕,当![]() 时,每日的销售额
时,每日的销售额![]() (单位:万元)与当日的产量
(单位:万元)与当日的产量![]() 满足
满足![]() ,当日产量超过20吨时,销售额只能保持日产量20吨时的状况.已知日产量为2吨时销售额为4.5万元,日产量为4吨时销售额为8万元.
,当日产量超过20吨时,销售额只能保持日产量20吨时的状况.已知日产量为2吨时销售额为4.5万元,日产量为4吨时销售额为8万元.
(1)把每日销售额![]() 表示为日产量
表示为日产量![]() 的函数;
的函数;
(2)若每日的生产成本![]() (单位:万元),当日产量为多少吨时,每日的利润可以达到最大?并求出最大值.
(单位:万元),当日产量为多少吨时,每日的利润可以达到最大?并求出最大值.
(注:计算时取![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥P-ABC中,AC⊥BC,且,AC=BC=2,D,E分别为AB,PB中点,PD⊥平面ABC,PD=3.
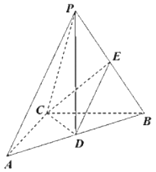
(1)求直线CE与直线PA夹角的余弦值;
(2)求直线PC与平面DEC夹角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com