【题目】已知椭圆：的中心为，一个方向向量为的直线与只有一个公共点

（1）若且点在第二象限，求点的坐标；

（2）若经过的直线与垂直，求证：点到直线的距离；

（3）若点、在椭圆上，记直线的斜率为，且为直线的一个法向量，且求的值.

【题目】某企业参加项目生产的工人为人，平均每人每年创造利润万元.根据现实的需要，从项目中调出人参与项目的售后服务工作，每人每年可以创造利润万元（），项目余下的工人每人每年创造利图需要提高

（1）若要保证项目余下的工人创造的年总利润不低于原来名工人创造的年总利润，则最多调出多少人参加项目从事售后服务工作？

（2）在（1）的条件下，当从项目调出的人数不能超过总人数的时，才能使得项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润，求实数的取值范围.

【题目】设，，其中m是不等于零的常数.

（1）时，直接写出的值域；

（2）求的单调递增区间；

（3）已知函数，，定义：，，，，其中，表示函数在上的最小值，表示函数在上的最大值.例如：，，则，，，.当时，恒成立，求n的取值范围.

【题目】设,,其中m是不等于零的常数,

(1)时,直接写出的值域;

(2)求的单调递增区间;

(3)已知函数(),定义:(),().其中,表示函数在D上的最小值,表示函数在D上的最大值.例如:,,则,,,.当时,设,不等式恒成立,求t,n的取值范围;

【题目】已知焦点在x轴上的双曲线C的两条渐近线过坐标原点，且两条渐近线与以点为圆心，1为半径的圆相切，又知C的一个焦点与P关于直线对称.

（1）求双曲线C的方程；

（2）设直线与双曲线C的左支交于A、B两点，另一直线经过及AB的中点，求直线在y轴上的截距b的取值范围；

（3）若Q是双曲线C上的任一点，、为双曲线C的左、右两个焦点，从引的角平分线的垂线，垂足为N，试求点N的轨迹方程.

【题目】已知函数.

(1)求函数的最小正周期并求出单调递增区间;

(2)在中,角A,B,C的对边分别是a,b,c,且满足,求的取值范围.

【题目】如图,已知直三棱柱中,,,,,点DE分别是边的中点,求:

(1)该直三棱柱的侧面积;

(2)异面直线与所成的角的大小(用反三角函数值表示)

【题目】已知数列和满足：，，，且对一切，均有.

（1）求证：数列为等差数列，并求数列的通项公式；

（2）若，求数列的前n项和；

（3）设（），记数列的前n项和为，问：是否存在正整数，对一切，均有恒成立.若存在，求出所有正整数的值；若不存在，请说明理由.

【题目】已知椭圆C：（）的焦距为，且右焦点F与短轴的两个端点组成一个正三角形.若直线l与椭圆C交于、，且在椭圆C上存在点M，使得：（其中O为坐标原点），则称直线l具有性质H.

（1）求椭圆C的方程；

（2）若直线l垂直于x轴，且具有性质H，求直线l的方程；

（3）求证：在椭圆C上不存在三个不同的点P、Q、R，使得直线、、都具有性质H.

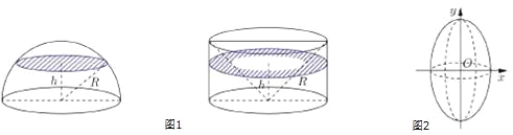
【题目】(数学文卷·2017届重庆十一中高三12月月考第16题) 现介绍祖暅原理求球体体积公式的做法：可构造一个底面半径和高都与球半径相等的圆柱，然后在圆柱内挖去一个以圆柱下底面圆心为顶点，圆柱上底面为底面的圆锥，用这样一个几何体与半球应用祖暅原理（图1），即可求得球的体积公式．请研究和理解球的体积公式求法的基础上，解答以下问题：已知椭圆的标准方程为 ，将此椭圆绕y轴旋转一周后，得一橄榄状的几何体（图2），其体积等于______．