
1、已知x、y是正变数,a、b是正常数,且 =1,x+y的最小值为__________.
=1,x+y的最小值为__________.
解析:令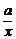 =cos2θ,
=cos2θ,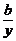 =sin2θ,则x=asec2θ,y=bcsc2θ,∴x+y=asec2θ+bcsc2θ=a+b+atan2θ+bcot2θ≥a+b+2
=sin2θ,则x=asec2θ,y=bcsc2θ,∴x+y=asec2θ+bcsc2θ=a+b+atan2θ+bcot2θ≥a+b+2 .答案:a+b+2
.答案:a+b+2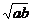
2、设正数a、b、c、d满足a+d=b+c,且|a-d|<|b-c|,则ad与bc的大小关系是__________.
解析:由0≤|a-d|<|b-c|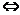 (a-d)2<(b-c)2
(a-d)2<(b-c)2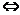 (a+b)2-4ad<(b+c)2-4bc
(a+b)2-4ad<(b+c)2-4bc
∵a+d=b+c,∴-4ad<-4bc,故ad>bc.答案:ad>bc
3、已知f(x)、g(x)都是奇函数,f(x)>0的解集是(a2,b),g(x)>0的解集是( ,
, ),
),
则f(x).g(x)>0的解集是__________.
解析:由已知b>a2∵f(x),g(x)均为奇函数,∴f(x)<0的解集是(-b,-a2),g(x)<0的解集是(-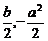 ).由f(x).g(x)>0可得:
).由f(x).g(x)>0可得:
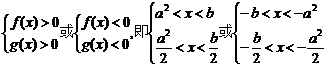
∴x∈(a2, )∪(-
)∪(- ,-a2)答案:(a2,
,-a2)答案:(a2, )∪(-
)∪(- ,-a2)
,-a2)
4、已知关于x的方程sin2x+2cosx+a=0有解,则a的取值范围是__________.
原方程可化为cos2x-2cosx-a-1=0,令t=cosx,得t2-2t-a-1=0,原问题转化为方程t2-2t-a-1=0在[-1,1]上至少有一个实根.令f(t)=t2-2t-a-1,对称轴t=1,画图象分析可得 解得a∈[-2,2].答案:[-2,2]
解得a∈[-2,2].答案:[-2,2]
5、已知函数f(x)=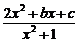 (b<0)的值域是[1,3],则b=
c= 。
(b<0)的值域是[1,3],则b=
c= 。
解:设y= ,则(y-2)x2-bx+y-c=0
①
,则(y-2)x2-bx+y-c=0
①
∵x∈R,∴①的判别式Δ≥0,即 b2-4(y-2)(y-c)≥0,即4y2-4(2+c)y+8c+b2≤0 ②
由条件知,不等式②的解集是[1,3]∴1,3是方程4y2-4(2+c)y+8c+b2=0的两根
 ∴c=2,b=-2,b=2(舍)
∴c=2,b=-2,b=2(舍)
6、直线2x-y-4=0上有一点P,它与两定点A(4,-1),B(3,4)的距离之差最大,
则P点坐标是_________.
解析:找A关于l的对称点A′,A′B与直线l的交点即为所求的P点.答案:P(5,6)
7、自点A(-3,3)发出的光线l射到x轴上,被x轴反射,其反射光线所在直线与
圆x2+y2-4x-4y+7=0相切,则光线l所在直线方程为_________.
解析:光线l所在的直线与圆x2+y2-4x-4y+7=0关于x轴对称的圆相切.
答案:3x+4y-3=0或4x+3y+3=0
8、函数f(θ)= 的最大值为_________,最小值为_________.
的最大值为_________,最小值为_________.
解析:f(θ)= 表示两点(cosθ,sinθ)与(2,1)连线的斜率.答案:
表示两点(cosθ,sinθ)与(2,1)连线的斜率.答案: 0
0
9、设不等式2x-1>m(x2-1)对一切满足|m|≤2的值均成立,则x的范围为_________.
原不等式变为(x2-1)m+(1-2x)<0,构造线段f(m)=(x2-1)m+1-2x,-2≤m≤2,
则f(-2)<0,且f(2)<0.答案:
10、已知椭圆的焦点是F1、F2,P是椭圆上的一个动点,如果延长F1P到Q,使得|PQ|=|PF2|,那么动点Q的轨迹是 。
解析:∵|PF1|+|PF2|=2a,|PQ|=|PF2|,∴|PF1|+|PF2|=|PF1|+|PQ|=2a,
即|F1Q|=2a,∴动点Q到定点F1的距离等于定长2a,故动点Q的轨迹是圆.
11、设A1、A2是椭圆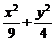 =1的长轴两个端点,P1、P2是垂直于A1A2的弦的端点,则直线A1P1与A2P2交点的轨迹方程为 。
=1的长轴两个端点,P1、P2是垂直于A1A2的弦的端点,则直线A1P1与A2P2交点的轨迹方程为 。
解析:设交点P(x,y),A1(-3,0),A2(3,0),P1(x0,y0),P2(x0,-y0)
∵A1、P1、P共线,∴ ∵A2、P2、P共线,∴
∵A2、P2、P共线,∴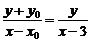
解得x0=
12、△ABC中,A为动点,B、C为定点,B(-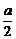 ,0),C(
,0),C(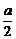 ,0),且满足条件sinC-sinB=
,0),且满足条件sinC-sinB= sinA,则动点A的轨迹方程为_________.
sinA,则动点A的轨迹方程为_________.
解析:由sinC-sinB= sinA,得c-b=
sinA,得c-b= a,
a,
∴应为双曲线一支,且实轴长为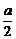 ,故方程为
,故方程为 .
.
答案:
13、中心在原点,焦点在坐标为(0,±5 )的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为
)的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为 ,则椭圆方程为(
)
,则椭圆方程为(
)

解析:由题意,可设椭圆方程为: =1,且a2=50+b2,
即方程为
=1,且a2=50+b2,
即方程为 =1.
=1.
将直线3x-y-2=0代入,整理成关于x的二次方程.
由x1+x2=1可求得b2=25,a2=75.答案:C
14、抛物线y=ax2与直线y=kx+b(k≠0)交于A、B两点,且此两点的横坐标分别为x1,x2,直线与x轴交点的横坐标是x3,则恒有( )
A.x3=x1+x2 B.x1x2=x1x3+x2x3 C.x1+x2+x3=0 D.x1x2+x2x3+x3x1=0
解析:解方程组 ,得ax2-kx-b=0,可知x1+x2=
,得ax2-kx-b=0,可知x1+x2= ,x1x2=-
,x1x2=- ,x3=-
,x3=- ,
,
代入验证即可.答案:B
15、已知A、B、C三点在曲线y= 上,其横坐标依次为1,m,4(1<m<4),当△ABC的面积最大时,m等于( )
上,其横坐标依次为1,m,4(1<m<4),当△ABC的面积最大时,m等于( )
A.3 B.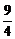 C.
C.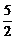 D.
D.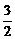
解析:由题意知A(1,1),B(m, ),C(4,2).直线AC所在方程为x-3y+2=0,
),C(4,2).直线AC所在方程为x-3y+2=0,
点B到该直线的距离为d=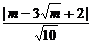 .
.
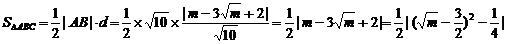
∵m∈(1,4),∴当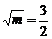 时,S△ABC有最大值,此时m=
时,S△ABC有最大值,此时m=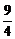 .答案:B
.答案:B
16、直线l的方程为y=x+3,在l上任取一点P,若过点P且以双曲线12x2-4y2=3的焦点作椭圆的焦点,那么具有最短长轴的椭圆方程为_________.
解析:所求椭圆的焦点为F1(-1,0),F2(1,0),2a=|PF1|+|PF2|.欲使2a最小,只需
在直线l上找一点P.使|PF1|+|PF2|最小,利用对称性可解.答案: =1
=1
17、双曲线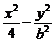 =1(b∈N)的两个焦点F1、F2,P为双曲线上一点,
=1(b∈N)的两个焦点F1、F2,P为双曲线上一点,
|OP|<5,|PF1|,|F1F2|,|PF2|成等比数列,则b2=_________.
解析:设F1(-c,0)、F2(c,0)、P(x,y),则|PF1|2+|PF2|2=2(|PO|2+|F1O|2)<2(52+c2),
即|PF1|2+|PF2|2<50+2c2,又∵|PF1|2+|PF2|2=(|PF1|-|PF2|)2+2|PF1|.|PF2|,
依双曲线定义,有|PF1|-|PF2|=4,依已知条件有|PF1|.|PF2|=|F1F2|2=4c2
∴16+8c2<50+2c2,∴c2< ,又∵c2=4+b2<
,又∵c2=4+b2< ,∴b2<
,∴b2< ,∴b2=1.答案:1
,∴b2=1.答案:1
18、正方形ABCD的边AB在直线y=x+4上,C、D两点在抛物线y2=x上,
则正方形ABCD的面积为_________.
解析:设C、D所在直线方程为y=x+b,代入y2=x,利用弦长公式可求出|CD|的长,
利用|CD|的长等于两平行直线y=x+4与y=x+b间的距离,求出b的值,
再代入求出|CD|的长. 答案:18或50
19、A是椭圆长轴的一个端点,O是椭圆的中心,若椭圆上存在一点P,使
∠OPA= ,则椭圆离心率的范围是_________.
,则椭圆离心率的范围是_________.
解析:设椭圆方程为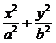 =1(a>b>0),以OA为直径的圆:x2-ax+y2=0,两式联立消y得
=1(a>b>0),以OA为直径的圆:x2-ax+y2=0,两式联立消y得 x2-ax+b2=0.即e2x2-ax+b2=0,该方程有一解x2,一解为a,
x2-ax+b2=0.即e2x2-ax+b2=0,该方程有一解x2,一解为a,
由韦达定理x2= -a,0<x2<a,即0<
-a,0<x2<a,即0< -a<a
-a<a <e<1.答案:
<e<1.答案: <e<1
<e<1
20、已知抛物线y=x2-1上一定点B(-1,0)和两个动点P、Q,当P在抛物线上运动时,
BP⊥PQ,则Q点的横坐标的取值范围是_________.
解析:设P(t,t2-1),Q(s,s2-1)∵BP⊥PQ,∴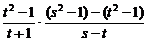 =-1,即t2+(s-1)t-s+1=0∵t∈R,∴必须有Δ=(s-1)2+4(s-1)≥0.即s2+2s-3≥0,解得s≤-3或s≥1.
=-1,即t2+(s-1)t-s+1=0∵t∈R,∴必须有Δ=(s-1)2+4(s-1)≥0.即s2+2s-3≥0,解得s≤-3或s≥1.
21、设f(x)=ax2+bx+c,若f(1)= ,问是否存在a、b、c∈R,使得不等式:
,问是否存在a、b、c∈R,使得不等式:
x2+ ≤f(x)≤2x2+2x+
≤f(x)≤2x2+2x+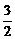 对一切实数x都成立,证明你的结论.
对一切实数x都成立,证明你的结论.
解:由f(1)= 得a+b+c=
得a+b+c= ,令x2+
,令x2+ =2x2+2x+
=2x2+2x+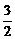 x
x =-1,由f(x)≤2x2+2x+
=-1,由f(x)≤2x2+2x+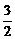 推得
推得
f(-1)≤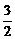 .由f(x)≥x2+
.由f(x)≥x2+ 推得f(-1)≥
推得f(-1)≥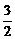 ,∴f(-1)=
,∴f(-1)=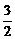 ,∴a-b+c=
,∴a-b+c=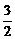 ,
,
故2(a+c)=5,a+c=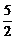 且b=1,∴f(x)=ax2+x+(
且b=1,∴f(x)=ax2+x+(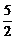 -a).依题意:ax2+x+(
-a).依题意:ax2+x+(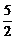 -a)≥x2+
-a)≥x2+
对一切x∈R成立,∴a≠1且Δ=1-4(a-1)(2-a)≤0,得(2a-3)2≤0,
∴f(x)=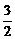 x2+x+1易验证:
x2+x+1易验证: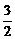 x2+x+1≤2x2+2x+
x2+x+1≤2x2+2x+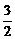 对x∈R都成立.
对x∈R都成立.
 ∴存在实数a=
∴存在实数a=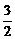 ,b=1,c=1,使得不等式:x2+
,b=1,c=1,使得不等式:x2+ ≤f(x)≤2x2+2x+
≤f(x)≤2x2+2x+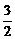 对一切x∈R都成立.
对一切x∈R都成立.
22、已知A、B、C是直线l上的三点,且|AB|=|BC|=6,⊙O′切直线l于点A,又过B、C作⊙O′异于l的两切线,设这两切线交于点P,求点P的轨迹方程.
解:设过B、C异于l的两切线分别切⊙O′于D、E两点,两切线交于点P.由切线的性质知:|BA|=|BD|,|PD|=|PE|,|CA|=|CE|,故|PB|+|PC|=|BD|+|PD|+|PC|=|BA|+|PE|+|PC|=|BA|+|CE|=|AB|+|CA|=6+12=18>6=|BC|,故由椭圆定义知,点P的轨迹是以B、C为两焦点的椭圆,以l所在的直线为x轴,以BC的中点为原点,建立坐标系,可求得动点P的轨迹方程为 =1(y≠0)
=1(y≠0)
23、 已知圆C1的方程为(x-2)2+(y-1)2=
已知圆C1的方程为(x-2)2+(y-1)2= ,椭圆C2的方程为
,椭圆C2的方程为 =1(a>b>0),C2的离心率为
=1(a>b>0),C2的离心率为 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程.
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程.
解:由e= ,可设椭圆方程为
,可设椭圆方程为 =1,又设A(x1,y1)、B(x2,y2),则x1+x2=4,y1+y2=2,
=1,又设A(x1,y1)、B(x2,y2),则x1+x2=4,y1+y2=2,
又 =1,两式相减,得
=1,两式相减,得 =0,
=0,
即(x1+x2)(x1-x2)+2(y1+y2)(y1-y2)=0.化简得 =-1,
=-1,
故直线AB的方程为y=-x+3,代入椭圆方程得3x2-12x+18-2b2=0.
有Δ=24b2-72>0,又|AB|=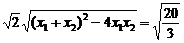 ,
,
得 ,解得b2=8.故所求椭圆方程为
,解得b2=8.故所求椭圆方程为 =1.
=1.
24、已知抛物线y2=2px(p>0),过动点M(a,0)且斜率为1的直线l与该抛物线交于不同的两点A、B,且|AB|≤2p. (1)求a的取值范围.
(2)若线段AB的垂直平分线交x轴于点N,求△NAB面积的最大值.

解:(1)设直线l的方程为:y=x-a,代入抛物线方程得(x-a)2=2px,即x2-2(a+p)x+a2=0
∴|AB|= ≤2p.∴4ap+2p2≤p2,即4ap≤-p2
≤2p.∴4ap+2p2≤p2,即4ap≤-p2
又∵p>0,∴a≤- .
.
(2)设A(x1,y1)、B(x2,y2),AB的中点 C(x,y),
由(1)知,y1=x1-a,y2=x2-a,x1+x2=2a+2p,
则有x=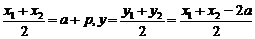 =p.
=p.
∴线段AB的垂直平分线的方程为y-p=-(x-a-p),从而N点坐标为(a+2p,0)
点N到AB的距离为
从而S△NAB=
当a有最大值- 时,S有最大值为
时,S有最大值为 p2.
p2.
25、已知双曲线C的两条渐近线都过原点,且都以点A( ,0)为圆心,1为半径的圆相切,双曲线的一个顶点A1与A点关于直线y=x对称. (1)求双曲线C的方程.
,0)为圆心,1为半径的圆相切,双曲线的一个顶点A1与A点关于直线y=x对称. (1)求双曲线C的方程.
(2)设直线l过点A,斜率为k,当0<k<1时,双曲线C的上支上有且仅有一点B到直线l的距离为 ,试求k的值及此时B点的坐标.
,试求k的值及此时B点的坐标.
解:(1)设双曲线的渐近线为y=kx,由d= =1,解得k=±1.
=1,解得k=±1.
即渐近线为y=±x,又点A关于y=x对称点的坐标为(0, ).
).
∴a= =b,所求双曲线C的方程为x2-y2=2.
=b,所求双曲线C的方程为x2-y2=2.
(2)设直线l:y=k(x- )(0<k<1
)(0<k<1 ,依题意B点在平行的直线l′上,
,依题意B点在平行的直线l′上,
且l与l′间的距离为 .
.
设直线l′:y=kx+m,应有 ,化简得m2+2
,化简得m2+2 km=2. ②
km=2. ②
把l′代入双曲线方程得(k2-1)x2+2mkx+m2-2=0,
由Δ=4m2k2-4(k2-1)(m2-2)=0.可得m2+2k2=2 ③
②、③两式相减得k= m,代入③得m2=
m,代入③得m2= ,解设m=
,解设m= ,k=
,k= ,此时x=
,此时x= ,y=
,y= .故B(2
.故B(2 ,
, ).
).