
2006年广州市番禺区九年级数学综合训练
一、选择题(本大题共10小题,每小题3分,满分30分.在每小题给出的四个选项中,只有一项是符合题目要求的,请选出来,填入下表中相对应的表格.)
1. 若家用电冰箱冷藏室的温度是
(A)-
2.用两个全等的三角形最多能拼成(※)个不同的平行四边形.
(A) 1 (B)2 (C)3 (D) 4
 3.计算
3.计算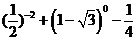 得( ).
得( ).
(A) (B)
(B)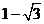 (C)
(C) (D)
(D)
4. 如右图所示,△ABC是顶角为32o的等腰三角形,将△ABC绕
点C旋转,使BC落在AC边上,则其旋转的角度为( ).
A.32o B.64o C.74o D.80o
5. 在一个花布袋中,装有4个玻璃珠,其中两个红色,两个蓝色,除颜色外其余特征均相同,若从这个袋子中,任取两个玻璃珠,得到都是蓝色玻璃珠的概率是( ).
(A)  (B)
(B) 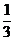 (C)
(C)
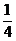 (D)
(D) 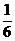
6. 某同学画出了下图中几何体模型的三种视图,每种视图分别标上代号(如图所示).
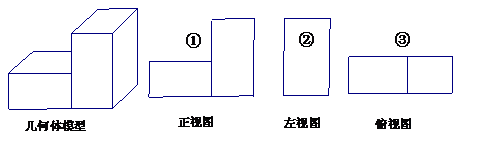 |
在这三个视图中,正确的有( ).
(A)①② (B)①③ (C)②③ (D)②
7. 已知点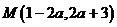 在第二象限,则a的取值范围是(
).
在第二象限,则a的取值范围是(
).
(A)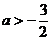 (B)
(B)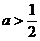 (C)
(C) (D)
(D)
8. 顺次连结等腰梯形各边中点所得到的四边形是( ).
(A)菱形 (B)矩形 (C)正方形 (D)梯形
9. 观察下列算式: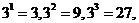
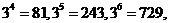 ……,用你发现的规律确定
……,用你发现的规律确定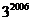 的个位数字是( ).
的个位数字是( ).
(A)1 (B)3 (C) 7 (D)9
10.若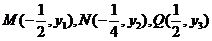 三点都在函数
三点都在函数 的图象上,则成立的是( ).
的图象上,则成立的是( ).
(A)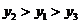 (B)
(B)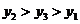 (C)
(C)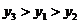 (D)
(D)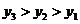
第二部分非选择题(共120分)
二、填空题(共6题,每题3分,共18分,直接把最简答案填写在题中的横线上)
11. 函数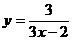 中自变量x的取值范围是
;
中自变量x的取值范围是
;
12. 用同一种正多边形的地砖镶嵌成平整的地面,那么这种正多边形地砖的形状可以是 ________________(只需写出一种即可);
13. 要了解我区九年级学生的视力状况,你认为合适的调查方式是________________;
14. 已知抛物线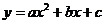 的顶点坐标为(1,0),并且经过点(0,-1),则此抛物线的解析式为: ________________;
的顶点坐标为(1,0),并且经过点(0,-1),则此抛物线的解析式为: ________________;
15. 如图,⊙M与x 轴相交于点A(2,0),B(8,0),与y轴相切于点C,则圆心M的坐标是________________;
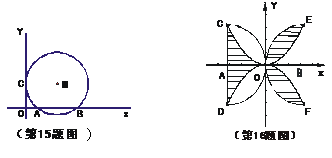 16. 如图,半径为
16. 如图,半径为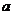 的半圆
的半圆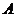 和半圆
和半圆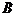 都与
都与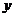 轴相切于坐标原点
轴相切于坐标原点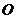 ,其直径
,其直径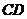 、
、 均与
均与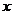 轴垂直,又以
轴垂直,又以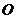 为顶点的两条抛物线恰好分别经过点
为顶点的两条抛物线恰好分别经过点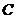 、
、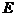 和点
和点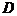 、
、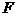 ,则图中阴影部分的面积为_________.
,则图中阴影部分的面积为_________.
三、解答题(本大题共9小题,满分102分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分9分)
化简、求值: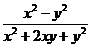 ,其中
,其中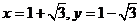 .
.
18.(本小题满分9分)
在南区公园的一片开阔草地中有一个小湖,在小湖的两侧各有一棵大树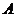 、
、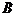 ,现要测量出
,现要测量出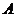 、
、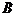 间的距离,但无法直接丈量.秦明同学用所学勾股定理的知识,设计了一种测量方案:
间的距离,但无法直接丈量.秦明同学用所学勾股定理的知识,设计了一种测量方案:
如图①,在草地上选取一点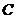 ,使点
,使点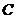 到点
到点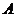 、
、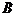 间的距离可测量,且
间的距离可测量,且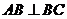 ,丈量出
,丈量出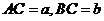 ,则由勾股定理得:
,则由勾股定理得: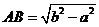 .
.
试利用你所学过的数学知识,再设计出两种不同的测量方案(要求:画出草图,写出计算公式,并标明公式中每个字母的实际意义).

.
解:方案一:
方案二:
19.(本小题满分10分,每小题5分)
(1)在实数范围内分解因式:
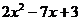 .
.
(2)解不等式组: ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.

20.(本小题满分10分)
如图,AB切⊙O于点B,OA交⊙O于C点,过C作DC⊥OA交AB于D,且BD:AD=1:2
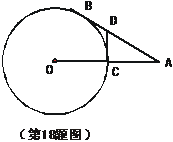 (1)求
(1)求 A的值.
A的值.
(2)若OC =1,求AB及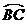 的长.
的长.
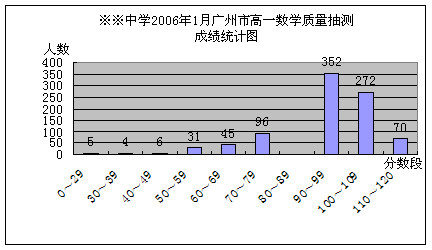 21. (本小题满分12分)
21. (本小题满分12分)
某高级中学高一年级共
有1141名同学,今年一月
参加了广州市数学质量
抽测,右图是学生测试
成绩的统计图(分数全
是整数,满分120分).
请根据以上信息完成
下列问题:
(1) 试将统计图补
充完整;
(2)求学生成绩的中位数落在哪一个分数段内?
(3)以90分(含90)以上的成绩定为优秀,据统计广州此次质量抽测的优秀率((优秀人数÷总人数)×100%))为25%,试问该中学此次高一成绩的优秀率超过全市平均水平多少个百分点?
22. (本小题满分12分)
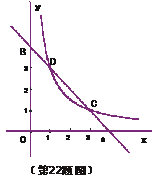 如图,已知直线
如图,已知直线 与双曲线
与双曲线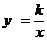 (
( )相交于C、D两点,且点C的坐标为
)相交于C、D两点,且点C的坐标为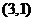 .
.
(1)求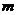 的值和双曲线的解析式;
的值和双曲线的解析式;
(2)观察直线的图象写出: 当 时,
时,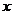 的取值范围;
的取值范围;
(3)观察双曲线的图象写出:当 时,
时,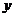 的取值范围.
的取值范围.
23. (本小题满分12分)
为了缓解电力紧张局面,电力公司鼓励工厂错峰用电,规定:每天0:00至7:00的时间为用电平稳时段,电价为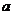 元/度,每天7:00至24:00为用电高峰时段,电价为
元/度,每天7:00至24:00为用电高峰时段,电价为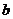 元/度.下表是红梅钢铁厂今年2、3月份的用电量与电费情况统计表:
元/度.下表是红梅钢铁厂今年2、3月份的用电量与电费情况统计表:
月份
用电量(万度)
电费(万元)
2
12
9.6
3
16
13.2
 (1)若2月份平稳时段的用电量占当月总用电量的
(1)若2月份平稳时段的用电量占当月总用电量的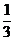 ,3月份平稳时段的用电量占当月总用电量的
,3月份平稳时段的用电量占当月总用电量的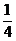 ,试求电价
,试求电价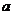 、
、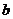 的值.
的值.
(2)该钢铁厂4月份计划用电20万度,要使电费支出不超过15万元,应如何安排用电计划?
24.(本小题满分14分)
如图,点 、
、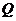 分别为等边
分别为等边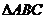 的两边
的两边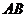 和
和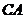 上的两个动点,
上的两个动点, 、
、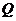 分别以相同的速度由
分别以相同的速度由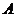 向
向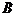 和由
和由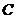 向
向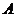 运动(不与端点重合),设
运动(不与端点重合),设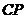 与
与 相交于
相交于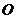 .
.
 (1)比较
(1)比较 与
与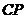 长的大小关系,并给予证明.
长的大小关系,并给予证明.
(2)当点 、
、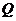 运动到何处时,
运动到何处时, 的周长
的周长
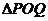 的周长的2倍?为什么?
的周长的2倍?为什么?
(3)探究点 、
、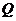 在运动过程中
在运动过程中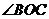 的大小怎样变化?
的大小怎样变化?
并对你的结论给予证明.
25.(本小题满分14分)
某中学一课外学习小组探究这样一个问题:现有一个长为
经过讨论,小组成员达成共识:在水流速度一定的情况下,水槽的横截面积越大,则通过水槽的流量越大.现假定你是该小组的成员,参与他们的探索活动:
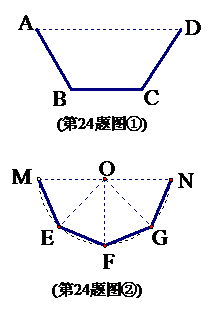
(1)方案甲,如图①把铁片扎制成等腰梯形水槽, . 设
. 设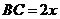 ┩,梯形
┩,梯形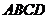 (水槽的横截面)的面积为
(水槽的横截面)的面积为 ,试写出
,试写出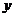 关于
关于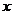 的函数关系式以及自变量
的函数关系式以及自变量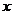 的取值范围,并求出
的取值范围,并求出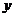 的最大值;
的最大值;
(2)小组成员王芳同学进一步探究后说:“方案乙: 把水槽的横截面扎制成如图②所示的形状,其中点 、
、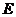 、
、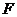 、
、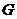 、
、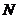 在以
在以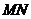 为直径的半圆周上,
为直径的半圆周上,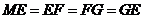 =
=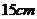 .此时,截面
.此时,截面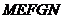 的面积
的面积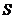 比方案甲中
比方案甲中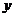 的最大值更大”,她的说法正确吗?为什么?
的最大值更大”,她的说法正确吗?为什么?
(3)你能找到一种使水槽的横截面面积比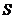 更大的设计方案吗?若能,请画出图形,标出必要的数据(可不写解答过程),写出你所设计方案的横截面面积;若不能,请说明理由。
更大的设计方案吗?若能,请画出图形,标出必要的数据(可不写解答过程),写出你所设计方案的横截面面积;若不能,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com