
浙江省杭绍金温衢七校2008学年高二第二学期期中联考试卷
数学(理科)
命 题:韩子荣 审 核:许唯唯
考试时间:120分钟 总 分:150分
第Ⅰ卷
一、选择题(本大题共10小题,每小题5分,共50分.每小题有且只有一个选
1.抛物线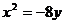 的准线方程是( ).
的准线方程是( ).
A.  B.
B. 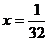 C.
C. D.
D.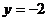
2.已知命题 则
则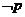 是( )
是( )
A. B.
B.
C.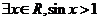 D.
D.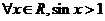
3.双曲线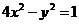 的渐近线方程是( )
的渐近线方程是( )
A.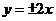 B.
B. 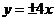 C.
C. 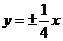 D.
D. 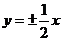
4.已知△ABC的三个顶点为A(3,3,2),B(4,-3,7),C(0,5,1),则
BC边上的中线长为( )
A.2
B.
5.若 ,则“
,则“ ”是“方程
”是“方程 表示双曲线”的( )
表示双曲线”的( )
A.充分不必要条件. B.必要不充分条件.
C.充要条件 D.既不充分也不必要条件
6.曲线 在点
在点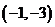 处的切线方程是 ( )
处的切线方程是 ( )
A.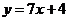 B.
B. C.
C.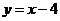 D.
D.
7.直线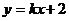 与抛物线
与抛物线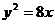 有且只有一个公共点,则
有且只有一个公共点,则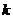 的值是( )
的值是( )
A.1 B.1或
8.已知椭圆 的左、右焦点分别为F1、F2,点P在椭圆上,若
的左、右焦点分别为F1、F2,点P在椭圆上,若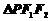
为直角三角形,则点P到x轴的距离为( )
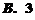
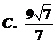
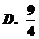
9.已知圆x2+y2=4,过A(4,0)作圆的割线ABC,则弦BC中点的轨迹方程是( )
A.(x-2)2+y2=4 B.(x-2)2+y2=4(0≤x<1)
C.(x-1)2+y2=4 D.(x-1)2+y2=4(0≤x<1)
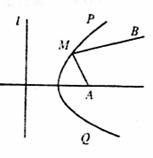 10.如图,l表示南北方向的公路,A地在公路的正东
10.如图,l表示南北方向的公路,A地在公路的正东
30°方向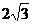 km处,河流沿岸PQ(曲线)上任一点到公
km处,河流沿岸PQ(曲线)上任一点到公
路l和到A地距离相等,现要在河岸PQ上选一处M建
一座码头,向A、B两地转运货物,经测算从M到A、B
修建公路的费用均为a万元/km,那么修建这两条公路的
总费用最低是(单位万元)( )
A.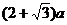 B.
B.
C.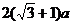 D.
D.
第Ⅱ卷
二、填空题:(本大题共7个小题,每小题4分,共28分.)
11.已知 , 且
, 且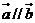 , 则
, 则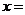 .
.
12. 在高台跳水运动中,运动员相对于水面的高度h (单位:m) 与起跳后的时间t (单位:s) 存在关系h
( t ) = -4.9 t 2
+ 6.5 t + 10,则起跳后1s的瞬时速度是 .
在高台跳水运动中,运动员相对于水面的高度h (单位:m) 与起跳后的时间t (单位:s) 存在关系h
( t ) = -4.9 t 2
+ 6.5 t + 10,则起跳后1s的瞬时速度是 .
 13.
13.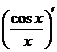 =_________________.
=_________________.
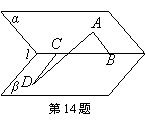
14.如图,二面角α-l-β的棱l上有两点B、C,AB⊥l,
CD⊥ l,且AB 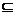 α ,CD
α ,CD 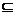 β
,若AB
= CD = BC =2,
β
,若AB
= CD = BC =2,
AD=4,则此二面角的大小为 .
15.已知圆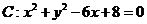 .以圆
.以圆 与坐标轴
与坐标轴
的交点分别作为双曲线的一个焦点和顶点,则适合上述条件的双曲线的标准方程为 .
16.倾斜角为60°的一束平行光线,将一个半径为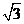 的球投影在水平地面上,形成一个椭圆,则此椭圆的离心率为
.
的球投影在水平地面上,形成一个椭圆,则此椭圆的离心率为
.
17.已知等边三角形的一个顶点位于抛物线 的焦点,另外两个顶点在抛物线上,则这个等边三角形的边长为 .
的焦点,另外两个顶点在抛物线上,则这个等边三角形的边长为 .
三、解答题:(本大题共5小题,共72分.请写出必要的文字说明或演算步骤)
18.(本题满分12分)
已知命题 :双曲线
:双曲线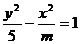 的离心率
的离心率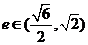 ,命题
,命题 :方程
:方程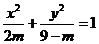 表示焦点在y轴上的椭圆.
表示焦点在y轴上的椭圆.
(1)若命题p是真命题,求实数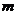 的取值范围;
的取值范围;
(2)若命题“ ∧
∧ ”是真命题,求实数
”是真命题,求实数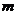 的取值范围.
的取值范围.
19.(本题满分15分)
 在平行六面体ABCD ? A1B
在平行六面体ABCD ? A1B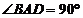 ,
,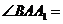
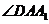
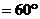 .若
.若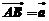 ,
,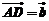 ,
,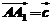
(1)用基底 表示向量
表示向量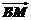 ;
;
(2)求向量 的长度.
的长度.
20.(本题满分15分)
如图所示,F1、F2分别为椭圆C: 的左、右两个焦点,A、B为两个顶点,已知椭圆C上的点
的左、右两个焦点,A、B为两个顶点,已知椭圆C上的点 到F1、F2两点的距离之和为4.
到F1、F2两点的距离之和为4.
(1)求椭圆方程和焦点坐标;
(2)过椭圆焦点F2作AB的平行线交椭圆于P、Q两点,求△F1PQ的面积.

21.(本题满分15分)
已知等腰梯形ABCD的上底AB=3,下底CD=1,高DO=1.以高线DO为折痕,将平面ADO折起,使得平面ADO⊥平面BCDO,点H为棱AC的中点.
(1)求直线OC与直线AB所成的余弦值;
(2)求平面ADO与平面ACB所成的锐二面角的余弦值;
(3)在平面ADO内找一点G,使得GH⊥平面ACB.
 |
|