
科目:gzsx 来源:甘肃省2012届高三第一次高考诊断数学试题 题型:044
设椭圆![]() 的右焦点为F1,直线
的右焦点为F1,直线![]() 与x轴交于点A,若
与x轴交于点A,若![]() +
+![]() =0(其中O为坐标原点)
=0(其中O为坐标原点)
(1)求椭圆M的方程;
(2)设点P是椭圆M上的任意一点,线段EF为圆N:x2+(y-2)2=1的任意一条直径(E、F为直径的两个端点),求![]() ·
·![]() 的最大值.
的最大值.
科目:gzsx 来源:甘肃省2012届高三第一次高考诊断数学试题 题型:044
设椭圆![]() 的右焦点为F,直线
的右焦点为F,直线![]() 与x轴交于点A,若
与x轴交于点A,若![]() +2
+2![]() =0(其中O为坐标原点)
=0(其中O为坐标原点)
(1)求椭圆M的方程;
(2)设点P是椭圆M上的任意一点,线段EF为圆N:x2+(y-2)2=1的任意一条直径(E、F为直径的两个端点),求![]() ·
·![]() 的最大值.
的最大值.
科目:gzsx 来源:2010-2011学年山西省忻州市高三第一次联考数学理卷 题型:解答题
(本题满分12分)
已知椭圆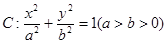 的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
(1)求椭圆C的方程;
(2)过点(4,0)且不与坐标轴垂直的直线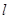 交椭圆
交椭圆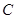 于
于 、
、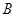 两点,设点
两点,设点 关于
关于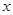 轴的对称点为
轴的对称点为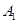 .求证:直线
.求证:直线 过
过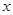 轴上的一定点,并求出此定点坐标.
轴上的一定点,并求出此定点坐标.
科目:gzsx 来源: 题型:
(本题满![]() 分12分)
分12分)
已知椭圆![]() 的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
(1)求椭圆C的方程;
(2)过点(4,0)且不与坐标轴垂直的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,设点
两点,设点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .求证:直线
.求证:直线![]() 过
过![]() 轴上的一定点,并求出此定点坐标.
轴上的一定点,并求出此定点坐标.
科目:gzsx 来源:山东省济宁市鱼台二中2011-2012学年高二3月月考数学文科试题 题型:044
已知,椭圆C以过点A(1,![]() ),两个焦点为(-1,0)(1,0).
),两个焦点为(-1,0)(1,0).
(1)求椭圆C的方程;
(2)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值.
科目:gzsx 来源:广东省深圳高级中学2011-2012学年高二上学期期末数学文科试题 题型:044
已知椭圆C过点A(1,![]() ),两个焦点为(-1,0),(1,0).
),两个焦点为(-1,0),(1,0).
(1)求椭圆C的方程;
(2)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值.
科目:gzsx 来源:2009年高考数学文科(辽宁卷) 题型:044
已知,椭圆
C以过点A(1,(1)求椭圆C的方程;
(2)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值.
科目:gzsx 来源: 题型:
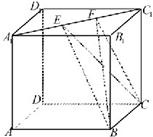 如图,正方体ABCD-A1B1C1D1的棱长为a,线段B1C上有一个动点P线段A1C1有两个动点E、F,且EF=
如图,正方体ABCD-A1B1C1D1的棱长为a,线段B1C上有一个动点P线段A1C1有两个动点E、F,且EF=
| ||
| 2 |
科目:gzsx 来源: 题型:
| x2 | 4 |
科目:gzsx 来源: 题型:
| ||
| 2 |
| 3 |
科目:gzsx 来源:2011-2012学年陕西省西安市五校联考高三第一次模拟考试理科数学 题型:选择题
椭圆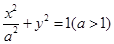 上存在一点P,使得它对两个焦点
上存在一点P,使得它对两个焦点 ,
, 张角
张角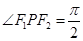 ,则该椭圆的离心率的取值范围是(
)
,则该椭圆的离心率的取值范围是(
)
A.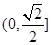 B.
B. C.
C.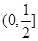 D.
D.
科目:gzsx 来源:2011-2012学年吉林省高三第六次模拟考试文科数学试卷(解析版) 题型:选择题
椭圆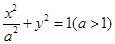 上存在一点P,使得它对两个焦点
上存在一点P,使得它对两个焦点 ,
, 的张角
的张角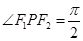 ,则该椭圆的离心率的取值范围是
,则该椭圆的离心率的取值范围是
A. B.
B. C.
C. D.
D.
科目:gzsx 来源:2011-2012学年山东省烟台市高三下学期3月诊断性测试文科数学 题型:选择题
椭圆 上存在一点P,使得它对两个焦点
上存在一点P,使得它对两个焦点 ,
, 的张角
的张角 ,则该椭圆的离心率的取值范围是
,则该椭圆的离心率的取值范围是
A.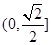 B.
B. C.
C. D.
D.
科目:gzsx 来源:2010-2011学年河北省高三上学期期末考试数学文卷 题型:解答题
((本小题满分12分)
中心在原点,焦点在x轴上的椭圆,率心率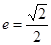 ,此椭圆与直线
,此椭圆与直线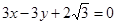 交于A、B两点,且OA⊥OB(其中O为坐标原点).
交于A、B两点,且OA⊥OB(其中O为坐标原点).
(1)求椭圆方程;
(2)若M是椭圆上任意一点, 、
、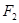 为椭圆的两个焦点,求
为椭圆的两个焦点,求 的取值范围;
的取值范围;
科目:gzsx 来源:2011-2012学年陕西省西安市高三下学期第一次模拟考试理科数学 题型:选择题
.椭圆 上存在一点P,使得它对两个焦点
上存在一点P,使得它对两个焦点 ,
, 张角
张角 ,则该椭圆的离心率的取值范围是(
)
,则该椭圆的离心率的取值范围是(
)
A. B.
B. C.
C. D.
D.