
科目:czsx 来源: 题型:解答题
 如图,已知抛物线y=
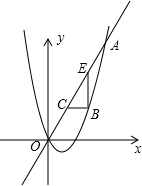
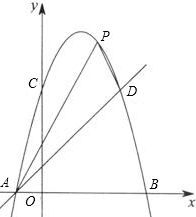
如图,已知抛物线y= x2+bx与直线y=2x交于点O(0,0),A(a,12).点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.
x2+bx与直线y=2x交于点O(0,0),A(a,12).点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.科目:czsx 来源:2013年浙江省丽水市中考数学试卷(解析版) 题型:解答题
 x2+bx与直线y=2x交于点O(0,0),A(a,12).点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.
x2+bx与直线y=2x交于点O(0,0),A(a,12).点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.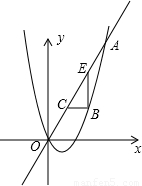
科目:czsx 来源: 题型:
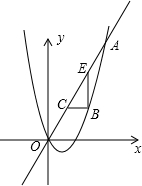 (2013•丽水)如图,已知抛物线y=
(2013•丽水)如图,已知抛物线y=| 1 | 2 |
科目:czsx 来源: 题型:
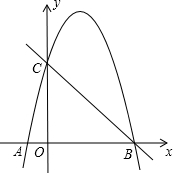
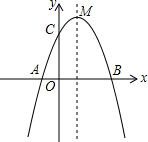 (2012•泰顺县模拟)如图,已知抛物线y=-x2+bx+c与x轴交于A、B(3,0)两点,与y轴交于点C(0,3).
(2012•泰顺县模拟)如图,已知抛物线y=-x2+bx+c与x轴交于A、B(3,0)两点,与y轴交于点C(0,3).科目:czsx 来源: 题型:
 如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C.
如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C.科目:czsx 来源: 题型:
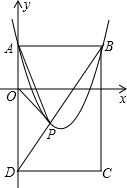 0,2),AB=4.
0,2),AB=4.| 3 | 2 |
科目:czsx 来源: 题型:
 ,
,| x1 |
| x2 |
| 1 |
| 3 |
| OE |
| 3 |
| 3 |
| 4 |
科目:czsx 来源: 题型:
| 9 | 2 |
科目:czsx 来源: 题型:
 如图,已知抛物线y=-x2+bx+c经过点A(-1,0)和C(0,4).
如图,已知抛物线y=-x2+bx+c经过点A(-1,0)和C(0,4).科目:czsx 来源: 题型:
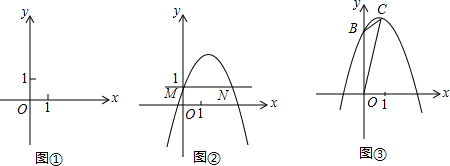
 如图,已知抛物线y=-x2+bx+c与x轴的两个交点分别为Α(1,0),B(3,0),
如图,已知抛物线y=-x2+bx+c与x轴的两个交点分别为Α(1,0),B(3,0),科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
 如图,已知抛物线y=-x2+bx+c与x轴交于点A、B两点,与y轴交于点C,其中A(1,0),C(0,-3).
如图,已知抛物线y=-x2+bx+c与x轴交于点A、B两点,与y轴交于点C,其中A(1,0),C(0,-3).科目:czsx 来源: 题型:
 且x1+x2=4,
且x1+x2=4,| x1 |
| x2 |
| 1 |
| 3 |
科目:czsx 来源: 题型:
 如图,已知抛物线y=x2+bx+c经过点(1,-5)和(-2,4)
如图,已知抛物线y=x2+bx+c经过点(1,-5)和(-2,4)| 5 |
科目:czsx 来源: 题型:
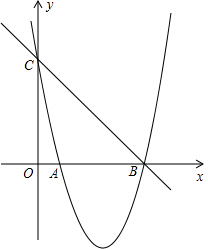 如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0).另一个交点为A,且与y轴交于点C(0,5).
如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0).另一个交点为A,且与y轴交于点C(0,5).科目:czsx 来源: 题型:
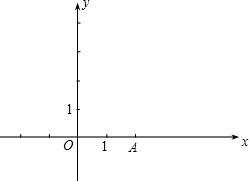 如图,已知抛物线 y=-x2+bx+c过点A(2,0),对称轴为y轴,顶点为P.
如图,已知抛物线 y=-x2+bx+c过点A(2,0),对称轴为y轴,顶点为P.科目:czsx 来源: 题型:
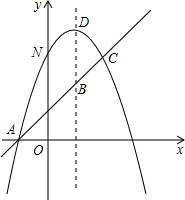 (2013•大兴区一模)如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
(2013•大兴区一模)如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N.其顶点为D.科目:czsx 来源: 题型:
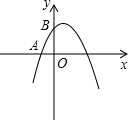 如图,已知抛物线y=-x2+bx+c与x轴负半轴交于点A,与y轴正半轴交于点B,且OA=OB.
如图,已知抛物线y=-x2+bx+c与x轴负半轴交于点A,与y轴正半轴交于点B,且OA=OB.科目:czsx 来源: 题型:
 如图,已知抛物线y=-x2+bx+c过点C,与x轴交于A,B两点,与y轴交于D点.
如图,已知抛物线y=-x2+bx+c过点C,与x轴交于A,B两点,与y轴交于D点.