
科目:gzsx 来源: 题型:
|
|
科目:gzsx 来源: 题型:
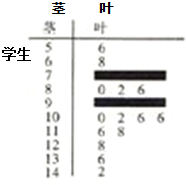 某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150] | 总计 |
| 频数 | b | |||||
| 频率 | a | 0.25 |
科目:gzsx 来源: 题型:
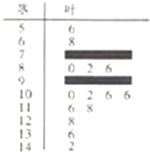 某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 总计 |
| 频数 | b | |||||
| 频率 | a | 0.25 |
科目:gzsx 来源:2014届河南省毕业班阶段测试一文数学卷(解析版) 题型:解答题
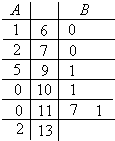
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
|
分数段(分) |
[50,70) |
[70,90) |
[90,110) |
[110,130) |
[130,150) |
总计 |
|
频数 |
|
|
|
b |
|
|
|
频率 |
a |
0.25 |
|
|
|
|

(1)求表中a,b的值及分数在[90,100)范围内的学生人数,并估计这次考试全校学生数学成绩的及格率(分数在[90,150)内为及格):
(2)从成绩大于等于110分的学生中随机选两人,求这两人成绩的平均分不小于130分的概率.
科目:gzsx 来源:2014届河南省毕业班阶段测试一理数学卷(解析版) 题型:解答题
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
|
分数段(分) |
[50,70) |
[70,90) |
[90,110) |
[110,130) |
[130,150) |
总计 |
|
频数 |
|
|
|
b |
|
|
|
频率 |
a |
0.25 |
|
|
|
|

(1)求表中a,b的值及分数在[90,100)范围内的学生人数,并估计这次考试全校学生数学成绩的及格率(分数在[90,150)内为及格):
(2)从成绩在[100,130)范围内的学生中随机选4人,
设其中成绩在[100,110)内的人数为X,求X的分布列及数学期望.
科目:gzsx 来源: 题型:
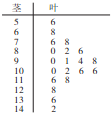 某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如下:
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如下:| 分数段(分) | [50,70] | [70,90] | [90,110] | [110,130] | [130,150] | 合计 |
| 频数 | b | |||||
| 频率 | a |
科目:gzsx 来源:2012-2013学年江苏省南通市高三第三次调研测试数学试卷(解析版) 题型:填空题
【江苏省南通市2013届高三第三次调研测试】在平面直角坐标系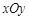 中,设点
中,设点 为圆
为圆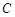 :
: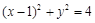 上的任意一点,点
上的任意一点,点 (2
(2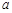 ,
,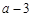 ) (
) ( ),则线段
),则线段 长度的最小值为 .
长度的最小值为 .
科目:gzsx 来源:2014届安徽省高三上学期第一次联考文科数学试卷(解析版) 题型:解答题
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取的20名学生的成绩进行分析,分数用茎叶图记录如下:

得到频率分步表如下:

(1)求表中 的值,并估计这次考试全校学生数学成绩及格率(分数在
的值,并估计这次考试全校学生数学成绩及格率(分数在 范围为及格);
范围为及格);
(2)从大于等于110分的学生中随机选2名学生得分,求2名学生的平均得分大于等于130分的概率.
科目:gzsx 来源:2014届安徽省高三上学期第一次联考理科数学试卷(解析版) 题型:解答题
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取的20名学生的成绩进行分析,分数用茎叶图记录如图所示(部分数据丢失),得到频率分布表如下:


(1)求表中 的值及分数在
的值及分数在 范围内的学生数,并估计这次考试全校学生数学成绩及格率(分数在
范围内的学生数,并估计这次考试全校学生数学成绩及格率(分数在 范围为及格);
范围为及格);
(2)从大于等于110分的学生中随机选2名学生得分,求2名学生的平均得分大于等于130分的概率.
科目:gzsx 来源: 题型:
 在2012年达州市高2013届第一次诊断性考试中,某校高2013届10班A、B两数
在2012年达州市高2013届第一次诊断性考试中,某校高2013届10班A、B两数. |
| xA |
| σ | 2 A |
. |
| xB |
| σ | 2 B |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
科目:gzsx 来源: 题型:
(09年湖南师大附中月考理)已知三条不重合的直线![]() ,两个不重合的平面
,两个不重合的平面![]() ,有下列命题:
,有下列命题:
①若![]() ∥
∥![]() ,
,![]()
![]()
![]() ,则
,则![]() ∥
∥![]() ; ②若
; ②若![]()
![]()
![]() ,
,![]()
![]()
![]() ,且
,且![]() ∥
∥![]() ,则
,则![]() ∥
∥![]()
③若![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() ∥
∥![]() ,则
,则![]() ∥
∥![]()
④若![]()
![]()
![]() ,
,![]()
![]()
![]() =
=![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,则
,则![]()
![]()
![]()
其中正确命题的个数为 ( )
A.1个 B.2个 C.3个 D.4个科目:gzsx 来源: 题型:
科目:gzsx 来源:2009-2010学年湖南师大附中高三(上)第三次月考数学试卷(理科)(解析版) 题型:解答题
科目:gzsx 来源:期末题 题型:解答题
科目:gzsx 来源:不详 题型:解答题
科目:gzsx 来源: 题型:解答题
科目:gzsx 来源:湖南省师大附中2010届高三第三次月考(理) 题型:解答题
为了参加师大附中第23届田径运动会的开幕式,高三年级某6个班联合到集市购买了6根竹竿,作为班旗的旗杆之用,它们的长度分别为3.8,4.3,3.6,4.5,4.0,4.1(单位:米).
(Ⅰ)若从中随机抽取两根竹竿,求长度之差不超过0.5米的概率;
(Ⅱ)若长度不小于4米的竹竿价格为每根10元,长度小于4米的竹竿价格为每根a元.从这6根竹竿中随机抽取两根,若期望这两根竹竿的价格之和为18元,求a的值.
科目:gzsx 来源: 题型:
(08年哈师大附中)高三某班50名学生参加某次数学模拟考试,所得的成绩(成绩均为整数)整理后画出的频率分布直方图如右图,则该班得120分以上的同学共有 人。

科目:gzsx 来源: 题型:
 前不久,省社科院发布了2013年度“安徽城市居民幸福排行榜”,芜湖成为本年度安徽最“幸福城”.随后,师大附中学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
前不久,省社科院发布了2013年度“安徽城市居民幸福排行榜”,芜湖成为本年度安徽最“幸福城”.随后,师大附中学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):